L’equazione di Bernoulli
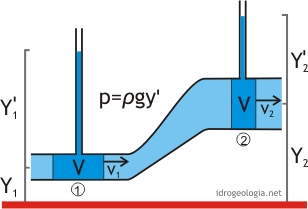
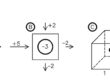
Fig. 1 – Un volume di fluido V si muove in un tubo nelle condizioni ideali dell’equazione di Bernoulli.
L’equazione di Bernoulli si applica a fluidi ideali, incomprimibili e non viscosi che si muovono con moto laminare.
In queste condizioni, posto che sia

facendo riferimento alla figura 1 vale la relazione
Visto che gli indici 1 e 2 si riferiscono a due punti generici, si può scrivere semplicemente
In queste condizioni se il fluido si muove in una condotta a sezione costante, e quindi se la velocità del fluido è uguale in tutti i punti della condotta, vale la relazione
Se lungo la condotta si realizzano dei tubi piezometrici, è possibile esprimere la pressione dell’acqua p in qualunque punto tramite la relazione
dove con y’ si indica la risalita dell’acqua all’interno del tubo piezometrico.
Applicando questa relazione si ricava quindi
e dividendo per ρּg si ottiene
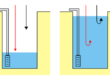
In realtà in una condotta a sezione costante con fluido in moto laminare la somma y’+y non è costante. Nei fluidi reali si osserva sperimentalmente che spostandosi nella direzione del movimento dell’acqua la somma y’+y tende progressivamente a diminuire. Questo fenomeno, rappresentato in figura 2a, è dovuto alla viscosità propria di tutti i fluidi reali. Per consentire il movimento delle particelle dell’acqua occorre vincere l’attrito dovuto alla viscosità e in questo processo si dissipa progressivamente pressione.
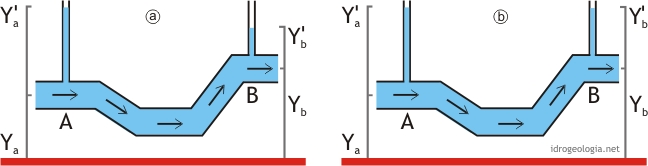
Fig. 2 – fluido ideale (b) e fluido reale (a) in movimento laminare in una condotta a sezione costante.
Facendo il ragionamento inverso, se nei punti A e B la somma fra altezza geometrica e altezza di pressione è constante (fig. 2b) significa che non non c’è dissipazione di pressione e quindi il fluido è in quiete. Se al contrario (fig. 2a) la somma y’+y non è costante, allora significa che esiste una dissipazione di pressione passando da A a B. Questo significa che esiste un flusso d’acqua diretto dal punto nel quale la somma fra y’ e y è maggiore (punto A) al punto nel quale la somma fra y’ e y è minore (punto B).
Si ha quindi
Applicazione dell’equazione di Bernoulli agli acquiferi
Negli acquiferi le velocità di spostamento dell’acqua sono di norma estremamente basse. Per questa ragione il termine
che compare nell’equazione di Bernoulli può essere trascurato in quanto molto piccolo se confrontato con gli altri termini.
In considerazione delle ridotte velocità di filtrazione, il ragionamento sviluppato in precedenza per la condotta a sezione costante può essere applicato anche al caso degli acquiferi. In pratica, nel caso della condotta a sezione costante il termine funzione della velocità viene eliminato in quanto costante in tutti i punti, mentre nel caso degli acquiferi viene eliminato perché, anche se variabile, è ovunque molto piccolo se paragonato agli altri due termini presenti nella formula.
Carico idraulico, altezza geometrica e altezza di pressione
Acquiferi con falda in quiete
Si definisce altezza di pressione di un determinato punto P dell’acquifero la pressione dell’acqua nel punto P misurata in metri di colonna d’acqua. Facendo riferimento alla figura 3a, si può immaginare di realizzare un piezometro con tratto filtrante in corrispondenza del punto P. La pressione dell’acqua in P, espressa in metri di colonna d’acqua, equivale al dislivello fra la quota raggiunta dall’acqua all’interno del tubo piezometrico e la quota del punto P. Nel caso dell’esempio, l’altezza di pressione in P equivale a 2 metri di colonna d’acqua.
L’altezza geometrica di un determinato punto P è la quota del punto P rispetto ad un piano orizzontale preso convenzionalmente a riferimento come quota zero. In figura 3a questo piano è marcato con un tratto rosso e, facendo riferimento a questo piano, l’altezza geometrica del punto P equivale a 2 metri.
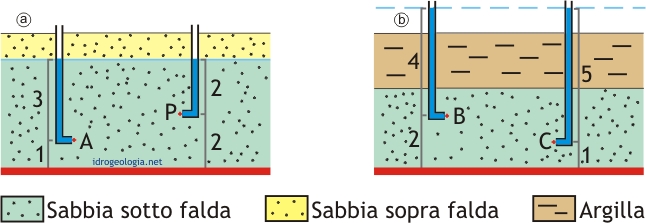
Fig. 3 – altezza geometrica e altezza di pressione. 1a: condizioni freatiche; 1b: condizioni artesiane.
Anche se da un punto di vista teorico sarebbe possibile scegliere qualunque piano come quota zero, per praticità come riferimento viene usualmente scelta la base dell’acquifero. In questo modo si evita che nel modello di filtrazione ci siano punti con altezza geometrica negativa.
In considerazione del fatto che le velocità di flusso dell’acqua in un acquifero sono di norma molto piccole, viene definito carico idraulico in un determinato punto P dell’acquifero la somma dell’altezza geometrica e dell’altezza di pressione del punto P.
![]()
Nel caso specifico del punto P il carico idraulico equivale a 2+2=4 metri.
Analogamente al caso di figura 2b, in un acquifero in quiete il valore del carico idraulico è uguale in tutti i punti. Immaginando infatti di ripetere il ragionamento precedente per il punto A di fig. 3a si otterrebbe una altezza di pressione di 3 metri, una altezza geometrica di un metro e un carico idraulico di 3+1=4 metri, uguale quindi a quello calcolato per il punto P.
Questo principio è valido anche se l’acquifero in quiete si trova in condizioni artesiane.
Facendo riferimento alla figura 3b si avrebbe infatti
| Punto | altezza di pressione | altezza geometrica | carico idraulico |
| B | 4 m | 2 m | 6 m |
| C | 5 m | 1 m | 6 m |
Dimensionalmente il carico idraulico è una lunghezza. Usualmente si misura in metri e viene indicato con la lettera h.
Acquiferi con falda in movimento
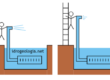
Se in un acquifero esistono punti a differente carico idraulico, si innesca un moto di filtrazione diretto dal punto a carico idraulico maggiore verso il punto a carico idraulico minore. Immaginando di disporre di uno strumento analogo a quello riportato in figura 4, posizionando la bacinella di destra alla medesima quota dello sfioratore del tubo di sinistra si uguagliano i carichi idraulici sulle superfici A e B del cilindro di sabbia. Poichè nel sistema non esiste alcuna differenza di carico idraulico, non si innesca alcun moto di filtrazione e l’acqua nel cilindro di sabbia permane in stato di quiete. Indicando con h il carico idraulico nei vari punti del sistema si ha quindi
Se si immagina di abbassare la bacinella B, si crea una differenza di carico idraulico alle estremità del cilindro. La differenza di carico idraulico innesca un moto di filtrazione, e di conseguenza una parte dell’acqua che si trova nel cilindro di sinistra transita attraverso il terreno e fuoriesce dalla bacinella di destra. Se si immagina di mantenere costante il livello dell’acqua nel cilindro di sinistra tramite alimentazione continua, si genera un moto di filtrazione stazionario diretto dalla superficie A alla superficie B del cilindro.
Sempre indicando con h il carico idraulico nel vari punti del sistema si ha:
La differenza di carico idraulico fra due punti viene definita perdita di carico idraulico o semplicemente perdita di carico e usualmente si indica con Δh.
La perdita di carico idraulico fra le superfici A e B del cilindro risulta quindi
Se si arresta l’alimentazione, in seguito al moto di filtrazione il livello dell’acqua nel cilindro di sinistra inizia lentamente a diminuire e di conseguenza diminuisce il carico idraulico sulla superficie A del cilindro. Nel momento in cui il livello nel cilindro scende fino alla quota del livello della bacinella di destra, si ripristina la condizione di uguaglianza dei carichi idraulici alle estremità del cilindro di sabbia. Il moto di filtrazione si arresta e il sistema ritorna nello stato di quiete.