La rete di flusso è una rappresentazione grafica che permette di visualizzare il moto di filtrazione in tutte le sue componenti. Questa tecnica è applicabile a flussi bidimensionali e stazionari in presenza di condizioni sia confinate sia non confinate. Utilizzando alcuni espedienti grafici questa tecnica è applicabile anche a mezzi anisotropi e, in alcune condizioni anche mezzi non omogenei.
Il procedimento matematico che porta alla definizione della rete di flusso è abbastanza complesso e passa per la risoluzione dell’equazione di Laplace [220, 232, 233, 517, 518]. Concentrandosi su alcuni semplici concetti di base dell’idrogeologia è comunque possibile capire il funzionamento di questo metodo di calcolo anche prescindendo dai rigorosi passaggi matematici.
Le linee equipotenziali, le linee di flusso e i tubi di flusso rappresentano i tre elementi alla base del disegno e la loro comprensione è fondamentale per l’applicazione di questa tecnica ai casi reali. In questa scheda vengono sviluppati questi tre concetti e per la lettura del testo si assume che siano conosciute le definizioni di {coefficiente di permeabilità} e di {carico idraulico}.
Le linee equipotenziali
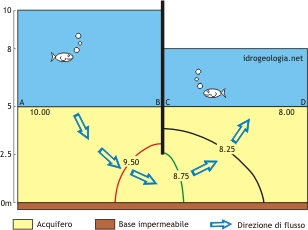
Fig. 1 – Le linee equipotenziali. In rosso, verde e nero sono indicate le linee equipotenziali con carico di 9,50, 8,75 e 8,25 metri. Come zero di riferimento è stata scelta la base dell’acquifero, indicato in giallo. In marrone è indicato il substrato impermeabile e con frecce azzurre è indicata la direzione di flusso dell’acqua
Il significato di linea equipotenziale può essere facilmente compreso considerando l’esempio classico della filtrazione al di sotto di una palancola. Con riferimento alla figura 1 si immagina che una palancola sia infissa nel terreno per una profondità pari a 2.5 metri in un acquifero con base a -5 metri da piano campagna. La palancola è infissa in una zona allagata e la quota dell’acqua è differente dai due lati. In particolare a sinistra della palancola l’acqua si trova ad una quota di +5 metri da p.c. mentre a destra si trova ad una quota di +3 metri da p.c. e il livello dell’acqua dai due lati si assume costante nel tempo. In queste condizioni si innesca un moto di filtrazione nel quale l’acqua transita da sinistra verso destra passando al di sotto della palancola. Posto che lo zero di riferimento sia fissato in corrispondenza della base dell’acquifero, in tutti i punti della linea AB il carico idraulico risulta ovunque uguale a 10 metri e in tutti i punti della linea CD il carico idraulico risulta ovunque uguale a 8 metri. Visto che l’acqua si sposta da AB verso CD, in tutta l’area interessata dalla filtrazione, che nella figura 1 corrisponde alla zona gialla, il carico idraulico assumerà valori compresi fra un massimo di 10 metri in prossimità della linea AB e un minimo di 8 metri in prossimità della linea CD. Per causa della differenza di livello dell’acqua dai due lati della palancola si instaura infatti un moto di filtrazione da AB verso CD e in questo processo, per vincere la forza di attrito opposta dal terreno si determina una progressiva dissipazione di carico idraulico. All’interno della regione interessata dalla filtrazione, se si collegano fra di loro tutti i punti caratterizzati dal medesimo carico idraulico, si ottiene una linea, che prende il nome di linea equipotenziale. Nel caso dell’esempio la linea rossa corrisponde alla linea equipotenziale con carico idraulico di 9,50 metri e questo significa che un piezometro, posizionato in qualunque punto lungo questa linea, rileverebbe un livello dell’acqua alla quota di 9,50 metri dallo zero di riferimento. Sempre facendo riferimento alla figura 1 la linea verde rappresenta la linea equipotenziale con carico idraulico di 8,75 metri e la linea nera l’equipotenziale con carico idraulico di 8,25 metri. All’interno della zona gialla di figura 1, interessata dal processo di filtrazione, è possibile tracciare infinite linee equipotenziali. Inoltre, visto che la linea AB ha carico idraulico di 10 metri, la linea CD ha carico idraulico di 8 metri e che la filtrazione è diretta da AB verso CD, spostandosi da sinistra verso destra le linee equipotenziali saranno caratterizzate da un carico idraulico via via decrescente.
Linee di flusso e tubi di flusso
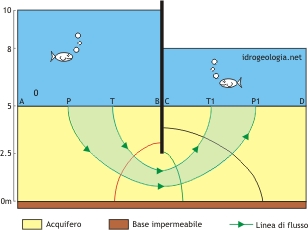
Fig. 2 – Linee di flusso e tubi di flusso. Con fondo azzurro è indicato il tubo di flusso compreso fra le linee di flusso PP1 e TT1. Le linee equipotenziali, riprese dalla figura 1, intersecano le linee di flusso formando angoli retti.
In presenza di moto laminare e di regime stazionario i percorsi di filtrazione non variano nel tempo. Facendo riferimento alla figura 2, in queste condizioni una particella che entra nell’acquifero nel punto P uscirà sempre nel punto P1 e una particella che entra nel punto T uscirà sempre nel punto T1. La linea PP1 e la linea TT1, che potremo immaginare come le tracce lasciate da una goccia di colorante lasciata cadere in P e in T, prendono il nome di linee di flusso. Visto che esistono infiniti punti lungo il segmento AB risulta intuitivo immaginare che è possibile tracciare infinite linee di flusso. La distanza fra due linee può variare, le linee si possono allontanare, avvicinare, arrivare quasi a sovrapporsi ma non si possono mai intersecare fra di loro. Se infatti si intersecassero una particella d’acqua, giunta al punto di intersezione, potrebbe ‘scegliere’ quale linea prendere per proseguire nel percorso di filtrazione e questo violerebbe quanto detto in precedenza.
Lo spazio compreso fra la linea PP1 e la linea TT1 viene chiamato tubo di flusso e questo nome deriva dal fatto che le due linee si comportano a tutti gli effetti come le pareti di un tubo: tutta l’acqua che entra nel tratto fra P e T deve infatti fuoriuscire nel tratto compreso fra P1 e T1. Visto che il moto si considera stazionario, la portata nel tubo di flusso non varia nel tempo. Il moto stazionario impone anche che non ci possa essere accumulo o cessione d’acqua lungo il tubo. Per questa ragione la portata in ogni sezione perpendicolare alle pareti del tubo deve essere le medesima.
Perpendicolarità fra linee di flusso e linee equipotenziali
Il moto di filtrazione può avvenire solamente in presenza di una differenza di carico idraulico. Nel caso dell’esempio di fig. 2 il moto di filtrazione avviene per via del fatto che la quota dell’acqua a sinistra della palancola è superiore alla quota dell’acqua a destra della palancola e quindi il carico idraulico lungo AB è superiore al carico idraulico lungo CD. All’interno del mezzo di filtrazione l’acqua si sposta da punti a carico idraulico più elevato verso punti a carico idraulico inferiore e quindi, facendo riferimento alla fig. 2, il flusso sarà diretto da AB (dove il carico idraulico è 10 metri) verso la linea equipotenziale rossa (9,50 metri) e da qui verso la linea equipotenziale verde (8,75 metri), quindi verso la linea equipotenziale nera (8,25 metri) e infine verso CD (dove il carico idraulico è 8 metri).
Visto che la perdita di carico è il presupposto fondamentale per la filtrazione, lungo una linea equipotenziale non ci può essere movimento d’acqua. Lungo una linea equipotenziale infatti il carico idraulico è costante in tutti i punti.
Proseguendo nel ragionamento, visto che la componente della velocità lungo la direzione della linea equipotenziale deve essere nulla ne consegue che le linee di flusso debbano essere perpendicolari alle linee equipotenziali.
In una regione interessata da una filtrazione è quindi possibile tracciare due famiglie di curve, fra di loro perpendicolari, chiamate linee equipotenziali e linee di flusso.