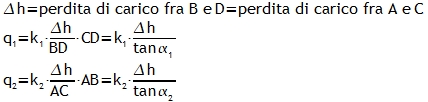La rete di flusso in mezzi anisotropi
Molti procedimenti utilizzati per la risoluzione di problemi di idrogeologia assumono un mezzo di filtrazione omogeneo e isotropo. Queste ipotesi sono spesso necessarie per poter semplificare le formule di calcolo ma non rispecchiano sempre in modo fedele le reali condizioni del terreno.
Una delle caratteristiche che di frequente si ritrova negli acquiferi reali è una anisotropia nel parametro coefficiente di permeabilità. Infatti, per via delle modalità di deposizione dei sedimenti, spesso gli acquiferi sono caratterizzati da una permeabilità orizzontale kh maggiore rispetto alla permeabilità verticale kv.
Il metodo di calcolo della rete di flusso permette di studiare la filtrazione anche in mezzi anisotropi, a condizione che si proceda con una opportuna deformazione geometrica. Questo metodo è riportato in molti testi e a titolo di esempio si possono citare [1]Braja M. Das (2008): Advanced soil mechanics. Routledge, pp 1-567 – ISBN 0415420261[2]Sarsby R.W. (2000): Environmental geotechnics. Thomas Telford, pp 1-584 – ISBN 0727727524[3]Harry R. Cedergren (1997): Seepage, Drainage, and Flow Nets. Wiley-IEEE, pp 1-496 – ISBN 047118053X[4]William Powrie (2004): Soil mechanics: concepts and applications. Taylor & Francis, pp 1-675 – ISBN 0415311551[5]H. M. Raghunath (1987): Ground Water. New Age International, pp 1-583 – ISBN 0852262981.
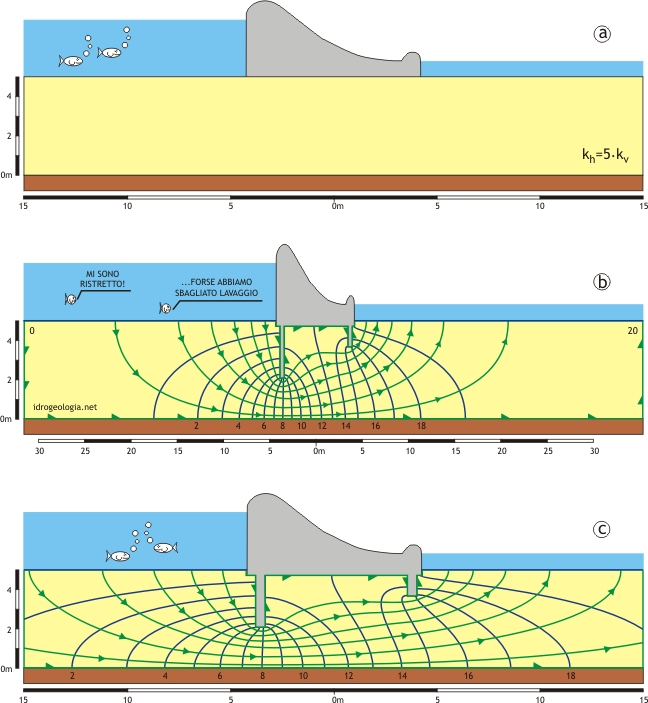
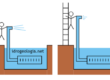
Fig. 1 – Disegno di una rete di flusso in un mezzo anisotropo. a) reale geometria del problema; b) deformazione geometrica necessaria per risolvere il problema utilizzando le regole di disegno della rete di flusso in mezzi isotropi; c) rideformazione del disegno per visualizzare il reale processo di filtrazione.
Ipotizzando che in un mezzo di filtrazione la permeabilità in senso orizzontale kh sia differente dalla permeabilità in senso verticale kv, per risolvere il problema è sufficiente deformare il modello in senso orizzontale di (kv/kh)0,5, disegnare la rete di flusso nel modello deformato utilizzando i criteri del disegno in condizione di mezzo isotropo e quindi rideformare tutto il disegno per riportarlo alle dimensioni iniziali.
Il procedimento può essere facilmente compreso esaminando i tre passaggi rappresentati in figura 1.
Si ipotizza che una traversa fluviale con due diaframmi sia realizzata in un mezzo anisotropo nel quale il coefficiente di permeabilità orizzontale sia 5 volte il coefficiente di permeabilità verticale (fig. 1a) e in queste condizioni si ricava un fattore di deformazione
Per disegnare la rete di flusso si crea una copia del disegno nella quale l’asse orizzontale viene deformato di 0,45 volte. Operando questa deformazione tutti gli elementi geometrici risultano ‘compressi’ in senso orizzontale (fig. 1b) e, per rendere ben evidente la deformazione, nella figura sono state riportate delle scale metriche di riferimento.
Utilizzando come riferimento la figura 1b si disegna la rete di flusso seguendo le regole valide i mezzi isotropi e si ottiene una rete a maglie quadrate.
Mediante questa rete si calcola la portata di filtrazione utilizzando però come valore di coefficiente di permeabilità la media geometrica dei coefficienti di permeabilità orizzontale e verticale.
facendo riferimento per semplicità un caso numerico, se
nelle condizioni indicate in figura 1b si ricaverebbe la seguente portata di filtrazione
Per riportare lo schema al caso reale occorre rideformare il disegno in modo che l’asse orizzontale ritorni alle sue originarie dimensioni e dopo questa operazione la rete di flusso risulta deformata. La rete deformata corrisponde alla reale rete di flusso nella quale le maglie non sono quadrate e le linee di flusso non risultano perpendicolari alle linee equipotenziali. Il passaggio intermedio di figura 1b è unicamente funzionale alla realizzazione del disegno e non rappresenta il reale andamento delle linee di flusso e delle linee equipotenziali. La portata di filtrazione può essere calcolata sia nelle condizioni deformate di fig. 1b sia nelle condizioni reali di figura 1d. In entrambe le figure i valori di Ne, Nf e Δh risultano infatti uguali e pertanto si perviene sempre al medesimo risultato.
La rete di flusso in mezzi non omogenei

Fig. 2 – Rete di flusso in un mezzo non omogeneo. In verde sono indicate le linee di flusso e in blu le linee equipotenziali. In grigio: mezzo meno permeabile (kmin) in giallo mezzo più permeabile (kMag). Nel caso rappresentato in figura kMag = 5·kmin.
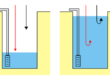
La rete di flusso può essere disegnata anche in presenza di un mezzo di filtrazione non omogeneo ma in questo caso occorre considerare che a parità di gradiente idraulico la portata è differente nei due mezzi. Pertanto, visto che in un tubo di flusso la portata per definizione deve essere costante, la spaziatura delle linee equipotenziali dovrà essere maggiore nel mezzo con coefficiente di permeabilità più elevato.
La figura 2 mostra uno stralcio di una rete di flusso tracciata al passaggio fra due mezzi caratterizzati da un differente coefficiente di permeabilità. In giallo è rappresentato il mezzo con coefficiente di permeabilità maggiore (kMag) e in grigio il mezzo con coefficiente di permeabilità minore (kmin). In particolare nel caso dell’esempio
Nel mezzo rappresentato in grigio è stata disegnata una rete di flusso a maglie quadrate con le linee di flusso indicate in verde e le equipotenziali indicate in blu.
Nel momento in cui le linee di flusso entrano nel mezzo colorato in giallo, con coefficiente di permeabilità più elevato, le maglie divengono rettangolari. In questi rettangoli il rapporto fra il lato rappresentato dal segmento di equipotenziale (blu) e il lato rappresentato dal segmento di linea di flusso (verde) è 1/5, pari cioè al rapporto fra kmin e kMag.
Questa deformazione consente di mantenere costante la portata nei tubi di flusso.
Con riferimento alla figura 2 e richiamandosi ai concetti illustrati nella scheda {disegnare una rete di flusso}, indicando rispettivamente con a e b i lati di una maglia costituiti dal segmento di equipotenziale e dal segmento di linea di flusso, si può scrivere
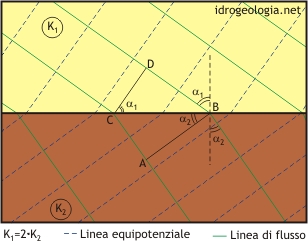
Figura 3 – calcolo dell’angolo di deviazione delle linee di flusso al passaggio fra due mezzi a differente coefficiente di permeabilità.
Visto che la differenza di carico idraulico alle estremità delle maglie è la medesima in tutto il modello e che e la maglia 1, realizzata nel mezzo meno permeabile, è quadrata, si ricava
Facendo riferimento all’esempio di figura 1, visto che kMag/kmin=5, nel mezzo a permeabilità maggiore si ottiene una rete di flusso rettangolare con il lato minore di lunghezza 5 volte inferiore rispetto al lato maggiore. Da un punto di vista pratico per disegnare una rete di flusso al passaggio fra due mezzi a differente permeabilità si applica una semplice regola matematica, riportata ad esempio in [6]Braja M. Das (2008): Advanced soil mechanics. Routledge, pp 1-567 – ISBN 0415420261[7]A S R Rao, Gopal Ranjan (2007): Basic and Applied Soil Mechanics. New Age International, pp 1-774 – ISBN 8122412238[8]U.S.A.C.E. (1993): Seepage analysis and control for dams. U.S. Army Corps of Engineers (Washington)[9]Robert V. Whitman, T. William Lambe (1969): Soil mechanics. John Wiley and Sons, pp 1-553 – ISBN 0471511927[10]Venkatramaiah C. (2006): Geotechnical Engineering. New Age International, pp 1-926 – ISBN 8122417930, che consente di calcolare l’angolo di deviazione delle linee di flusso al passaggio fra i due mezzi.
Facendo riferimento alla figura 3, al passaggio fra il mezzo a permeabilità maggiore k1, indicato in giallo, e il mezzo a permeabilità minore k2, indicato in marrone, le linee di flusso si flettono e di conseguenza la rete di flusso passa da una forma quadrata ad una forma rettangolare. La perdita di carico lungo il segmento DB è uguale alla perdita di carico lungo il segmento AC e pertanto, visto lungo un tubo di flusso non ci possono essere variazioni di portata, si può scrivere
visto che q1 deve essere uguale a q2 si ricava
Mediante questa equazione, noto il rapporto fra le permeabilità è possibile valutare la distorsione della rete di flusso nel punto di passaggio fra i due mezzi.
Bibliografia
| ↑1, ↑6 | Braja M. Das (2008): Advanced soil mechanics. Routledge, pp 1-567 – ISBN 0415420261 |
|---|---|
| ↑2 | Sarsby R.W. (2000): Environmental geotechnics. Thomas Telford, pp 1-584 – ISBN 0727727524 |
| ↑3 | Harry R. Cedergren (1997): Seepage, Drainage, and Flow Nets. Wiley-IEEE, pp 1-496 – ISBN 047118053X |
| ↑4 | William Powrie (2004): Soil mechanics: concepts and applications. Taylor & Francis, pp 1-675 – ISBN 0415311551 |
| ↑5 | H. M. Raghunath (1987): Ground Water. New Age International, pp 1-583 – ISBN 0852262981 |
| ↑7 | A S R Rao, Gopal Ranjan (2007): Basic and Applied Soil Mechanics. New Age International, pp 1-774 – ISBN 8122412238 |
| ↑8 | U.S.A.C.E. (1993): Seepage analysis and control for dams. U.S. Army Corps of Engineers (Washington) |
| ↑9 | Robert V. Whitman, T. William Lambe (1969): Soil mechanics. John Wiley and Sons, pp 1-553 – ISBN 0471511927 |
| ↑10 | Venkatramaiah C. (2006): Geotechnical Engineering. New Age International, pp 1-926 – ISBN 8122417930 |