Modello esemplificativo 3 x 3
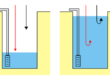
La Figura 7 mostra un esempio molto semplificato di modello Modflow, utile per comprendere il meccanismo di equilibrio della portata in ingresso e in uscita dalle singole celle. Il modello esemplificativo ha un solo layer, con 9 celle quadrate di lato 100. Si suppone che la conducibilità idraulica sia K=2 e lo spessore del modello sia uguale a 3 quindi, facendo riferimento alla Figura 6, Δv=3, Δc=100 e Δr=100.
Nel fornire le dimensioni e la conducibilità idraulica volutamente non si è fatto riferimento ad unità di misura: MODFLOW non usa unità di misura per eseguite i calcoli ma assume che le unità di misura inserite dal modellista siano consistenti. Pertanto, se le unità scelte per le distanze sono i metri e per i tempi i secondi, tutte le lunghezze andranno espresse in metri, la conducibilità idraulica in metri al secondo, le portate in metri cubi al secondo e la ricarica in metri al secondo. In questo modo i risultati ottenuti da MODFLOW saranno in metri per quello che riguarda il carico idraulico e in metri cubi al secondo per quello che riguarda le portate. Se vengono usate altre unità, ad esempio metri e anni, occorrerà esprimere la conducibilità in metri all’anno, le portate in metri cubi all’anno, la ricarica in metri all’anno e così via. Il suggerimento è di utilizzare sempre i metri per le lunghezze e i secondi per i tempi, in conformità con il sistema internazionale di unità di misura (SI).
Nell’esempio, per il quale si omette qualunque indicazione di unità di misura, si assume che nella cella Ca sia presente un lago con livello dell’acqua costante a quota 10 e nella cella Bc sia presente un pozzo che estrae una portata -6. Nel modello si instaurerà una filtrazione dal lago verso il pozzo con carichi idraulici che progressivamente diminuiranno dalla cella Ca alla cella Bc. L’unico carico idraulico noto è quello relativo alla cella Ca, in quanto in questa cella si immagina sia presente un lago con livello costante nel tempo, mentre in tutte le restanti celle il carico idraulico è ignoto. L’obiettivo di MODFLOW è esattamente la ricostruzione del carico in tutte le 8 restanti celle: noto il carico è possibile conoscere lo scambio idrico fra le celle del modello e definire l’andamento della piezometrica.
Per risolvere il problema MODFLOW procede per tentativi, andando a modificare il valore di tutte le celle del modello fintanto che, per ogni cella, si verifica un equilibrio fra le portate in ingresso e in uscita. In realtà l’equilibrio perfetto non si raggiunge mai e quindi MODFLOW considera risolto il problema quando l’errore è contenuto all’interno di una soglia definita dal modellista come accettabile.
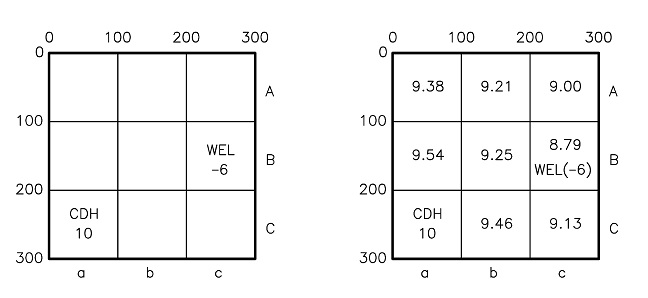
Figura 7 – Modello MODFLOW esemplificativo per visualizzare il procedimento del calcolo del carico idraulico nelle varie celle del modello.
L’immagine a destra in Figura 7 indica per ogni cella il valore di carico idraulico al termine dei tentativi, quando cioè MODFLOW ha trovato una serie di valori di carichi idraulici che soddisfano i criteri di chiusura impostati in fase di modellazione.
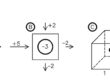
Facendo riferimento alla Figura 6, la portata di filtrazione fra due celle si può calcolare come q=K∙(h/Δr)∙( Δv∙Δc), con h corrispondente alla differenza di carico. Sostituendo i numeri alle variabili si ricava q= 6∙h.
Prendendo ad esempio la cella Ba si calcola una portata q=6∙(10-9.54)=+2.76 in ingresso dalla cella Ca, una portata q=-1.74 in uscita verso la cella Bb e una portata q=-0.96 in uscita verso la cella Aa. Il lato sinistro della cella Ba corrisponde al bordo del modello e quindi la portata in ingresso e in uscita da questo lato è nulla: i bordi del modello, come anche i contatti fra le celle attive e le celle inattive, sono considerati limiti impermeabili.
Sommando le tre portate con il loro segno si ricava Q=2.76-1.74-0.96=0.06, cioè circa zero. In realtà la precisione di un vero modello MODFLOW è superiore ma per l’esempio i valori di carico, e quindi gli errori associati, sono stati approssimati al secondo decimale.
Ripetendo il calcolo per la cella Aa si ricava Q=0.16∙6 – 0.17∙6=-0.06. In questo caso lo scambio avviene solamente da due lati in quanto la cella si trova in corrispondenza di uno spigolo del modello.
In modo analogo si può procedere con tutte le altre celle, verificando che l’equilibrio è ovunque raggiunto.
La cella Bc ha associata una condizione pozzo (WEL) che estrae una portata -6. Complessivamente, quindi, dalle 3 facce della cella deve entrare una portata 6, necessaria per consentire l’emungimento dal pozzo. Eseguendo il calcolo risulta infatti dalla cella Ac una portata q=1.26, da Bb q=2.76 e da Cc q=2.04. Complessivamente risulta Q= 1.26+2.76+2.04=6.06. Anche in questo caso il bilancio è raggiunto, a meno dell’errore accettabile.
La cella Ca è la cella nella quale si trova il lago che impone un carico idraulico noto, nell’esempio uguale a 10. Visto che il modello non solo deve trovare un equilibrio in ogni singola cella, ma deve trovare un equilibrio anche nella sua complessità, se dal pozzo esce una portata -6 dal lago deve entrare una portata 6. Traslato nella realtà si potrebbe dire che, per ottenere un sistema in equilibrio, se dal pozzo viene estratta una portata -6 dal lago deve percolare nell’acquifero una portata 6.
Eseguendo il calcolo relativamente alla cella Ca si ricava infatti una portata q=-2.76 verso la cella Ba e q= -3.24 verso la cella Cb per un totale Q=-6. Dalla cella Ca esce quindi una portata -6, che significa che dalla condizione al contorno CHD usata per simulare il lago entra una portata 6.
Una volta ottenuta la distribuzione dei carichi in tutte le celle del modello è possibile rappresentare graficamente le equipotenziali che, in una condizione di acquifero freatico, rappresentano le isofreatiche. Per ricavare una rappresentazione di questo tipo è sufficiente interpolare, ad esempio con il metodo dell’interpolazione triangolare, i valori ottenuti per le singole celle, immaginandoli applicati al centro delle celle stesse.
Le celle CHD, le celle no-flow e le celle variable-head
In MODFLOW le celle possono essere di tre tipi: variable-head, costant head e no-flow. Le celle di tipo variable-head sono sempre la stragrande maggioranza. Rappresentano tutte quelle celle per le quali il carico idraulico non è definito a priori ma deve essere ricavato da MODFLOW utilizzando il procedimento iterativo descritto in precedenza.
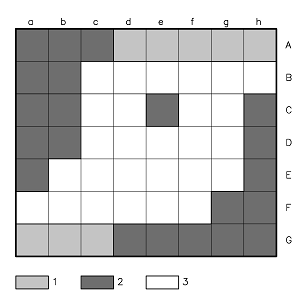
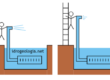
Figura 8 – Esempio ideale di modello di filtrazione con celle costant-head (1), celle no-flow (2) e celle variable-head (3).
Ad una cella variable-head può essere associata una o più condizioni al contorno.
Le celle di tipo costant-head sono celle per le quali il carico idraulico è noto in anticipo.
Una cella costant-head può, e di norma lo fa, scambiare acqua con celle adiacenti cioè da una cella costant-head di solito entra o esce acqua verso le celle confinanti del modello di flusso. Una cella costant-head ha associata una condizione CHD e per questo motivo cella costant-head e CHD vengono spesso utilizzati come sinonimi.
Le celle costant-head vengono ad esempio utilizzate per simulare delle condizioni al contorno del modello abbastanza distanti dall’area di studio e per le quali il carico idraulico è conosciuto.
A titolo di esempio una serie di celle costant-head potrebbe essere usata per simulare la presenza di un lago o per imporre ai bordi del modello una certa differenza di carico idraulico.
Le celle di tipo no-flow sono celle che vengono escluse dal processo di filtrazione. In una cella no flow non può né entrare né uscire acqua e pertanto una cella no-flow può essere considerata come un oggetto perfettamente impermeabile.
La Figura 8 mostra un caso ipotetico di griglia di modello di flusso con celle no-flow sui bordi utilizzate per sagomare l’area di modellazione. Una cella no-flow può trovarsi anche al centro del modello, per simulare ad esempio una struttura impermeabile.
In grigio chiaro sono indicate delle ipotetiche celle costant-head. In un caso di questo genere la condizione CHD della riga A avrà un carico idraulico associato differente dalla condizione CHD della riga G, generando in questo modo un flusso all’interno del modello.
Tutte le celle bianche sono invece celle variable-head.