Premessa
MODFLOW permette di risolvere problemi estremamente complessi, ma il suo principio di funzionamento è abbastanza semplice.
MODFLOW suddivide il volume di terreno interessato dalla modellazione in celle e di conseguenza in ogni cella l’acqua può entrare ed uscire solamente attraverso le facce della cella stessa.
Il flusso può essere in entrata, se diretto verso la cella, o in uscita, se diretto dalla cella verso l’esterno. I flussi in entrata si considerano positivi e quelli in uscita negativi.
Ciò premesso, in condizioni stazionarie per ogni cella del modello la somma delle portate in ingresso e delle portate in uscita, ognuna con il suo segno, deve essere uguale a zero mentre in condizioni transitorie la somma delle portate in ingresso e delle portate in uscita da ogni cella, ognuna con il suo segno, deve essere uguale al volume d’acqua immagazzinato o ceduto dalla cella nell’intervallo di tempo considerato.
Il bilancio di massa
Per riuscire a visualizzare il concetto con maggiore semplicità, si può immaginare che la filtrazione avvenga in condizioni stazionarie e che il modello abbia un solo layer, cioè che il flusso sia bidimensionale e si sviluppi sul piano x-y. Una volta compreso il funzionamento il questa modalità semplificata, si può facilmente estendere il ragionamento alle 3 dimensioni e alle condizioni transitorie.
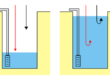
In Figura 6 sono indicati due esempi di celle in equilibrio. Nel caso A, in questa ideale cella di forma quadrata entra una portata +5 dal lato di sinistra ed esce una portata -2 e -3 dal lato inferiore e dal lato destro. In questo caso il bilancio è nullo in quanto se si sommano tutte le portate con il loro segno risulta q=5-2-3-0=0.
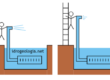
Ad alcune celle del modello possono essere associate delle condizioni particolari, per simulare pozzi, aree di ricarica, torrenti, ecc…. Una fra le condizioni più semplici e più comunemente utilizzate nei modelli MODFLOW è la condizione pozzo (WEL) che impone alla cella una determinata portata in uscita, che rappresenta la portata estratta dal pozzo.
In un caso di questo tipo, l’equilibrio verrà raggiunto quando la somma delle portate in entrata e in uscita dai lati della cella sarà uguale alla portata estratta dal pozzo. Facendo riferimento allo schema B, considerando che dal pozzo viene estratta una portata uguale a -3 risulta q=(5+2-2-2)-3=0.
In pratica, quindi, in condizioni stazionarie in ogni cella non ci deve essere nè accumulo nè cessione d’acqua.
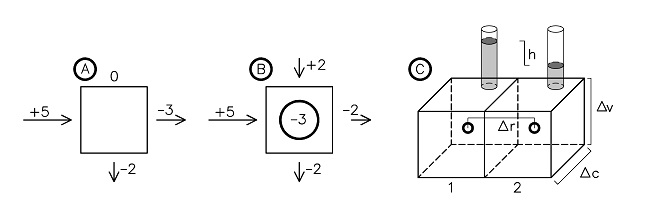
Figura 6 – Bilancio fra portate in ingresso e portate in uscita. A: cella senza alcuna condizione al contorno applicata; B: cella con applicata una condizione al contorno; C: calcolo della portata fra due celle adiacenti.
Questo ragionamento, illustrato per semplicità in uno schema piano, si riproduce in modo concettualmente identico in uno schema tridimensionale, semplicemente aggiungendo le portate in ingresso e in uscita verso la cella superiore e verso la cella inferiore.
Il calcolo della portata attraverso una faccia
Il calcolo della portata in ingresso e in uscita da una singola faccia della cella si calcola utilizzando l’equazione di base dell’idrogeologia Q=K∙i∙A.
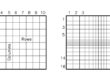
Facendo riferimento anche in questo caso a condizioni semplificate con un mezzo di filtrazione omogeneo, isotropo e completamente saturo, la portata di filtrazione fra due celle (schema C di Figura 6) si può calcolare come Q=K∙(h/Δr)∙( Δv∙Δc) dove K rappresenta la conducibilità idraulica del terreno, h la differenza di carico idraulico fra le due celle, Δv∙Δc l’area della sezione di filtrazione e Δr la distanza fra i centri delle due celle.
Esaminando l’equazione emerge che K è noto in quanto viene definito in fase di creazione del modello e Δr, Δv e Δc sono noti in quanto dipendono dalle caratteristiche della griglia, definita anch’essa in fase di creazione del modello.
L’unica variabile non conosciuta è rappresentata da h, cioè dalla differenza di carico idraulico fra le due celle. Se il carico idraulico della cella 1 è superiore al carico idraulico della cella 2, come da figura, il flusso è diretto dalla cella 1 alla 2; se il carico idraulico della cella 1 è uguale al carico idraulico della cella 2, h diviene uguale a 0 e il flusso attraverso la faccia di separazione delle due celle diventa nullo. A parità di altre condizioni, quindi, all’aumentare di h aumenta la portata attraverso le celle.