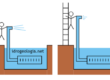
Lo schema più semplice da esaminare con il metodo della rete di flusso è la filtrazione attraverso un provino di terreno contenuto all’interno di un condotto a sezione quadrata o rettangolare e sottoposto ad una differenza di carico idraulico alle estremità. Lo schema, che concettualmente riproduce le condizioni presenti in un permeametro a carico costante, è rappresentato in figura 1.
In queste condizioni se h1 e h2 sono i carichi idraulici alle estremità del provino, L è la lunghezza del provino, A l’area e k il coefficiente di permeabilità, nell’ipotesi in cui h1>h2 si ricava facilmente la portata di filtrazione
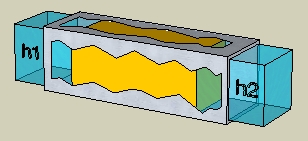
Fig. 1 – raffigurazione schematica di un provino di terreno (giallo) racchiuso in un tubo alle estremità del quale è applicata una differenza di carico idraulico Δh = h1-h2. Se h1>h2 l’acqua filtra da sinistra verso destra.
Facendo riferimento per semplicità ad un ipotetico caso reale in cui
si ricava
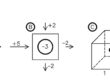
In questo semplice processo di filtrazione l’acqua fluisce dalla superficie di sinistra, a carico idraulico maggiore, verso la superficie di destra, a carico idraulico minore. Vista la geometria del sistema si intuisce facilmente che le linee di flusso sono tutte parallele fra di loro e pertanto il moto di filtrazione è di tipo monodimensionale. Delle tre componenti della velocità vx, vy e vz, solamente una è diversa da zero e pertanto il problema, che è un caso particolare del moto di filtrazione bidimensionale, può essere studiato mediante il metodo della rete di flusso.
In questo caso elementare il disegno della rete di flusso è facilitato dal fatto che la direzione delle linee di flusso è nota a priori. Queste infatti iniziano in corrispondenza della superficie a carico idraulico maggiore, terminano in corrispondenza della superficie a carico idraulico minore ed hanno un andamento perfettamente rettilineo.
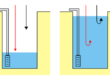
Nel caso dell’esempio, visto il rapporto di 0,30/0,80 fra altezza e larghezza del provino, può essere facilmente ottenuta una rete a maglie quadrate utilizzando 3 tubi di flusso e 8 linee equipotenziali (figura 2a).
L’equidistanza fra le linee equipotenziali in questo caso è uguale a
Applicando la formula per il calcolo della portata di una rete di flusso al caso di figura 2a e considerando che
si ricava
Moltiplicando questo valore per lo spessore del modello, che è di 0,3 metri, si ottiene la portata di filtrazione
uguale a quella ricavata in precedenza.
Problemi geometrici derivanti dalle dimensioni della maglia
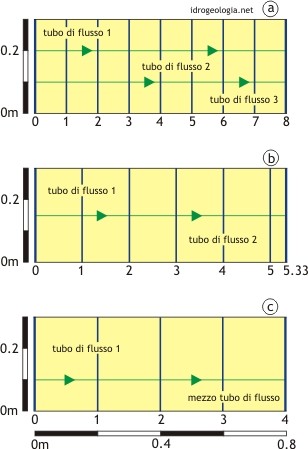
Fig. 2 – Esempi di rete di flusso nelle condizioni di filtrazione schematizzate nella figura 1. a) rete di flusso a maglie quadrate. b) rete di flusso con l’ultima serie di maglie rettangolari, c) rete di flusso con il tubo di flusso inferiore di spessore dimezzato.
Variando le dimensioni della maglia, cioè aumentando o diminuendo il numero di tubi di flusso o variando l’equidistanza fra le equipotenziali, il valore della portata resta ovviamente invariato. Tuttavia modificando la spaziatura fra le linee non è detto si riesca sempre ad ottenere una rete a maglie quadrate. L’esempio precedente, per via della sua semplicità, si presta bene a verificare questo aspetto.
La figura 1b mostra il modello risolto con soli 2 tubi di flusso. In questo caso per ottenere le maglie quadrate è necessario far si che l’ultima maglia all’estrema sinistra del modello diventi rettangolare. La geometria del sistema infatti non consente di suddividere il lato orizzontale del disegno in modo che risulti un multiplo esatto della metà del lato verticale e così, operando con due tubi di flusso, non è geometricamente possibile rendere quadrate tutte le maglie.
Il problema si risolve considerando che la lunghezza della linea di flusso dell’ultima maglia all’estrema destra è pari ad 1/3 della lunghezza che dovrebbe avere per risultare quadrata e quindi si considera che la perdita di carico fra le due ultime linee di flusso sia 1/3 dell’equidistanza fra le equipotenziali.
In pratica quindi Ne si considera uguale a 5 + 1/3 = 5,33 e con questa assunzione si procede con la formula utilizzata in precedenza ottenendo un risultato analogo a quello già calcolato
Un problema concettualmente identico si può porre si decide di iniziare il disegno tracciando prima le linee equipotenziali e poi le linee di flusso. Se ad esempio si inizia l’operazione di disegno tracciando 4 equipotenziali, ottenendo quindi una equidistanza di 0,5 metri/4 = 0,125 metri, non è più possibile realizzare due tubi di flusso a maglia quadrata. Il tubo inferiore infatti risulta con maglie rettangolari con altezza dimezzata (fig. 2c). Anche in questo caso si può comunque applicare la formula di base della rete di flusso, considerando però un numero di tubi di flusso Nf = 1 + 1/2 = 1,5.
Si ricava quindi
pervenendo ancora una volta al medesimo risultato.