I corpi geologici presenti in natura sono spesso stratificati e quindi costituiti da alternanze di livelli differenti per litologia e grado di cementazione. Da un punto di vista idrogeologico un terreno stratificato non può essere considerato omogeneo, in quanto ogni strato è caratterizzato da un suo proprio valore di permeabilità. La disomogeneità di permeabilità rappresenta un ostacolo alla risoluzione dei problemi di filtrazione e quindi usualmente si procede con una semplificazione.
Se un terreno è composto da un numero n di livelli sovrapposti ognuno caratterizzato da un valore di permeabilità kn e da uno spessore Dn, tramite alcuni passaggi matematici è possibile convertire questo mezzo non omogeneo in un equivalente mezzo omogeneo. Questo mezzo ha però la caratteristica di comportarsi in modo differente in funzione della direzione di flusso dell’acqua. Se viene attraversato dall’acqua in direzione parallela alla stratificazione opporrà una certa resistenza all’attraversamento, mentre se la filtrazione avviene in senso perpendicolare alla stratificazione opporrà una resistenza differente, di solito superiore. Un mezzo con questa caratteristica viene definito omogeneo ma anisotropo. In un mezzo di questo tipo occorrerà utilizzare un certo valore di coefficiente di permeabilità per lo studio di problemi nei quali la direzione di flusso è parallela alla stratificazione e un altro valore per lo studio dei problemi nei quali la direzione di flusso è perpendicolare ai piani di strato.
Il coefficiente di permeabilità orizzontale
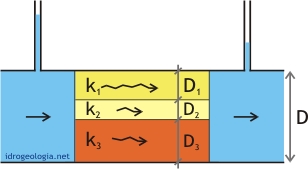
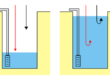
Fig. 1 – calcolo del coefficiente di permeabilità nella direzione parallela alla stratificazione (korizzontale)
Facendo riferimento alla figura 1, si immagina che il terreno sia attraversato da un flusso orizzontale. Se k1, k2 e k3 sono le permeabilità dei tre livelli sovrapposti di spessore D1, D2 e D3, visto che il gradiente i è il medesimo per i tre strati di terreno si può calcolare la portata di filtrazione attraverso ogni strato nel modo seguente:
Immaginando di sostituire il mezzo reale stratificato con un mezzo equivalente in cui il coefficiente di permeabilità in senso parallelo alla stratificazione sia kparallelo si ottiene:
Combinando le equazioni si ricava:
Dividendo entrambi i termini per i si ottiene infine:
Visto che nei terreni sciolti sede di falda acquifera la stratificazione è prevalentemente orizzontale o a basso angolo, il termine kparallelo si indica usualmente con korizzontale o con kh.
Si ricava quindi la formula generale:
dove Dn e kn indicano rispettivamente lo spessore e il coefficiente di permeabilità dell’ennesimo strato di terreno.
In un terreno stratificato, se il flusso è parallelo alla stratificazione la velocità di filtrazione è differente nei vari livelli. Visto infatti che:
se un livello è caratterizzato da una permeabilità doppia rispetto ad un altro anche le velocità di filtrazione saranno l’una il doppio dell’altra.
Il coefficiente di permeabilità verticale
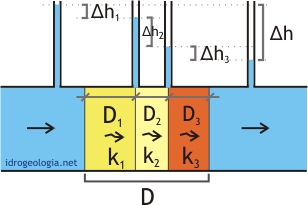
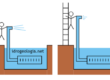
Fig. 2 – calcolo del coefficiente di permeabilità nella direzione perpendicolare alla stratificazione (kverticale)
Facendo riferimento alla figura 2, si immagina che il terreno sia attraversato da un flusso perpendicolare alla stratificazione. Visto che il flusso si suppone stazionario, la velocità di filtrazione deve essere uguale nei tre strati di terreno. Se infatti la velocità di filtrazione nel livello 1 fosse superiore alla velocità di filtrazione del livello 2, si avrebbe un accumulo di acqua nel secondo livello e questo non è possibile vista l’assunzione iniziale di moto stazionario. Se Δh1, Δh2 e Δh3 sono le perdite di carico alle estremità dei livelli 1, 2, 3, e se D1, D2 e D3 sono gli spessori di questi livelli, si possono definire i gradienti idraulici nei tre strati con le equazioni:
Visto che
si ricava
che definiremo Eq. 1.
Per la continuità del flusso la velocità di filtrazione deve essere uguale in tutti gli strati, e pertanto si può scrivere:
Immaginando di sostituire il mezzo reale stratificato con un mezzo equivalente in cui il coefficiente di permeabilità in senso perpendicolare alla stratificazione sia kperpendicolare si ottiene:
Combinando questa equazione con le tre equazioni delle velocità calcolate in precedenza si ricava:
e analogamente:
Inserendo i tre valori di i appena calcolati in quella che in precedenza era stata definita equazione 1 si ottiene:
![]()
Dividendo entrambi i termini per Δh e raccogliendo i termini kperpendicolare e D si ricava
e si previene infine all’equazione:
Visto che nei terreni sciolti sede di falda acquifera la stratificazione è prevalentemente orizzontale o a basso angolo, il termine kperpendicolare si indica usualmente con kverticale oppure con kv.
Si ricava pertanto la formula generale:
dove Dn e kn indicano rispettivamente lo spessore e il coefficiente di permeabilità dell’ennesimo strato di terreno.