In una regione interessata dalla filtrazione è possibile tracciare infinite linee di flusso e infinite linee equipotenziali. Utilizzando alcune regole geometriche è però possibile selezionane solo alcune e disegnare una maglia, chiamata rete di flusso, costruita con caratteristiche tali da poter essere utilizzata per il calcolo della portata di filtrazione e per altri calcoli idrogeologici.
Facendo riferimento alla figura 1, tracciate 4 equipotenziali qualunque si definisce:
Al fine di chiarezza, per non confondere le differenze di carico fra due linee equipotenziali contigue con le differenze di carico totali alle estremità del modello, le prime vengono identificate dal sovrasegno ^.
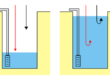
Facendo riferimento al tubo di flusso evidenziato in colore azzurro si assume che le due aree ottenute dall’intersezione delle linee di flusso con il tubo di flusso, marcate in figura con tratto spesso, siano assimilabili a due rettangoli. In queste condizioni è possibile calcolare la portata fra le linee I e II e fra le linee III e IV con le equazioni

Fig. 1 – Portata in un tubo di flusso. Con tratto spesso sono indicati due rettangoli curvilinei ottenuti dall’intersezione di due coppie di equipotenziali con le pareti del tubo di flusso. Il rapporto a1/b1 è differente dal rapporto a2/b2. Come conseguenza la differenza di carico idraulico fra le due coppie di equipotenziali è differente (9,75-9,50=0,25 m nella coppia di sinistra e 8,75-8,25=0,50 m nella coppia di destra)
Visto che lungo il tubo di flusso non ci può essere accumulo o cessione di acqua, la portata q1 deve risultare uguale a q2 e pertanto si ricava:
Se le linee equipotenziali vengono tracciate in modo che la perdita di carico fra due equipotenziali contigue sia sempre la medesima si ottiene
e pertanto in queste condizioni deve risultare
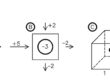
e nel caso dell’esempio di figura 2 questo rapporto è uguale a 0,5.
Disegnare una rete di flusso significa scegliere fra le infinite linee di flusso e le infinite linee equipotenziali quelle che consentono di suddividere la regione di filtrazione in una serie di rettangoli curvilinei in cui il rapporto fra il lato ottenuto dal segmento di equipotenziale e il lato ottenuto dal segmento di linea di flusso sia il medesimo per tutti i rettangoli.
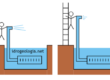
Il processo può essere facilmente compreso immaginando di percorrere i due passaggi illustrati nella figura 3.
Il primo passaggio consiste nel tracciamento di linee equipotenziali tracciate in modo che la perdita di carico fra due linee contigue sia sempre la medesima. Una volta tracciate queste linee si scelgono fra le infinite linee di flusso quelle che meglio consentono di ottenere una suddivisione dell’area in sagome rettangolari di uguali proporzioni. In questo caso, facendo riferimento alla figura 3b, si avrebbe a/b = 2.
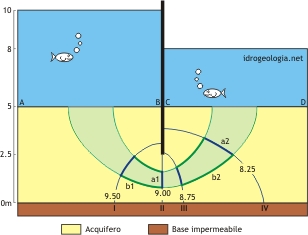
Fig. 2 – Portata in un tubo di flusso. Con tratto spesso sono indicati due rettangoli curvilinei ottenuti dall’intersezione di due coppie di equipotenziali con le pareti del tubo di flusso. Il rapporto a1/b1 è uguale al rapporto a2/b2.
La figura 3b mostra un esempio di rete di flusso a maglie rettangolari utilizzabile per calcolare la portata di filtrazione e valutare la distribuzione delle pressioni interstiziali nell’acquifero interessato dalla filtrazione. Nelle zone più esterne e nelle zone in prossimità della palancola la maglia risulta molto distorta. Questo è dovuto all’approssimazione del metodo e viene accettato come errore inevitabile.
Sebbene sia possibile disegnare reti di flusso a maglie rettangolari, nella pratica si preferisce utilizzare reti a maglie quadrate. La figura 4, nella quale
rappresenta lo stesso schema di filtrazione della figura 3b disegnato però con maglie quadrate.
La maglia quadrata rappresenta la forma più usuale di rete di flusso. Nel processo manuale di disegno, che viene eseguito per approssimazioni successive con la gomma e la matita, si è visto infatti che più semplice individuare delle forme quadrate piuttosto che forme rettangolari di uguali proporzioni.
In una rete di flusso a maglie quadrate il calcolo della portata di un tubo di flusso diviene immediato.
Facendo riferimento alla figura 4 si ha infatti
In una rete di flusso la perdita di carico fra due equipotenziali contigue è la medesima per tutto il modello
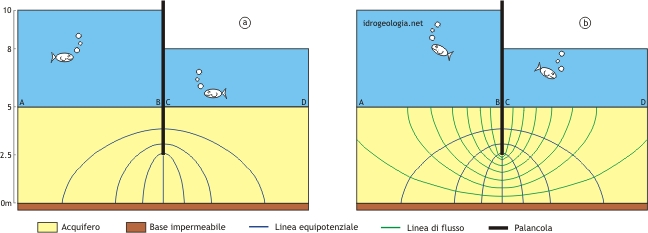
Figura 3 – Rete di flusso a maglie rettangolari: a) insieme delle linee equipotenziali con equidistanza uguale a 0,25 m. b) linee di flusso tracciate in modo da ottenere una suddivisione dell’area di filtrazione in sagome rettangolari. In ogni rettangolo il lato corrispondente al segmento di equipotenziale è approssimativamente la metà del lato corrispondente al segmento di linea di flusso.
e se la rete è a maglie quadrate vale anche la relazione
Si ricava pertanto l’equazione
che consente di calcolare la portata lungo un singolo tubo di flusso.
La differenza di carico fra due linee equipotenziali contigue è calcolabile conoscendo la differenza di carico complessiva alle estremità del modello e pertanto
dove
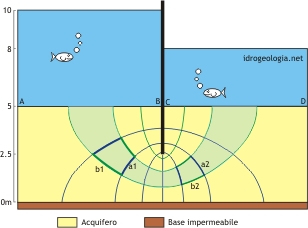
Fig. 4 – Filtrazione al di sotto della palancola rappresentata con una rete di flusso a maglie quadrate
La portata di filtrazione dell’intero modello è calcolabile semplice moltiplicando la portata del singolo tubo di flusso per il numero totale Nf dei tubi di flusso.
Si ottiene quindi
che rappresenta l’equazione fondamentale per il calcolo della portata mediante l’utilizzo della rete di flusso.
La rete di flusso viene utilizzata per lo studio di moti di filtrazione bidimensionali, nei quali cioè una delle tre componenti della velocità di filtrazione può essere considerata nulla. Per questa ragione qmodello ha le dimensioni [L2T-1].
Per ricavare la reale portata di filtrazione occorre quindi moltiplicare il valore ottenuto per lo spessore della struttura. Immaginando cioè che la palancola dell’esempio si sviluppi linearmente per una distanza L, trascurando gli effetti di bordo si otterrebbe quindi la portata di filtrazione compressiva