Le due condizioni al contorno più comuni nello studio dei problemi confinati sono rappresentate dai limiti a carico idraulico costante e dai limiti impermeabili. In questo tipo di problema il mezzo di filtrazione è completamente saturo e pertanto non è necessario definire l’andamento della superficie libera dell’acqua. Il disegno della rete di flusso risulta quindi facilitato in quanto è noto a priori che non esistono porzioni del modello insature. Alcuni esempi abbastanza classici di rete di flusso in condizioni confinate con mezzo di filtrazione omogeneo ed isotropo sono riportate in figura 1 e 2.
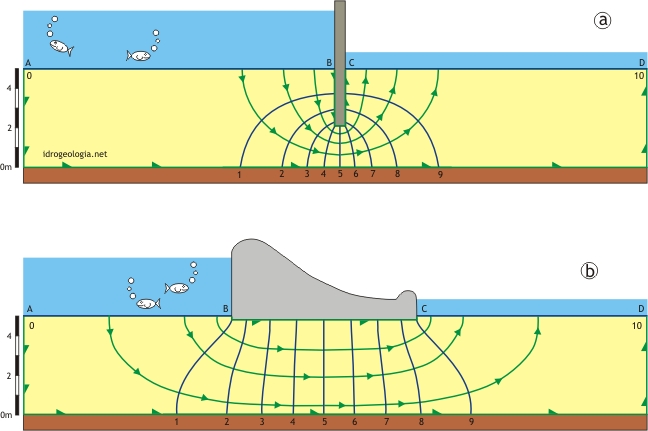
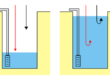
Fig. 1 – Esempi di reti di flusso in condizioni confinate con mezzo di filtrazione omogeneo ed isotropo. a) filtrazione al di sotto di una palancola, b) filtrazione al di sotto di una traversa fluviale senza diaframmi.
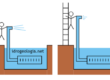
Nello specifico i casi illustrati riguardano la filtrazione al di sotto di una palancola che separa due zone allagate (1a), la filtrazione al di sotto di una traversa fluviale senza diaframmi (1b), la filtrazione la di sotto di una traversa con diaframmi (2a) e la filtrazione al di sotto di una traversa con diaframmi con base dell’acquifero irregolare (2b). In tutti questi casi si suppone che la struttura abbia uno sviluppo lineare tale da rendere trascurabili gli effetti di bordo e che sia pertanto possibile lo studio del problema in condizioni bidimensionali.
Nelle figure in colore verde sono indicate le linee equipotenziali e in colore blu le linee di flusso. Le condizioni al contorno a carico idraulico costante sono rappresentate dalle linee AB e CD mentre in colore marrone e grigio sono indicati rispettivamente la base dell’acquifero e l’opera di sbarramento, entrambe considerate impermeabili.
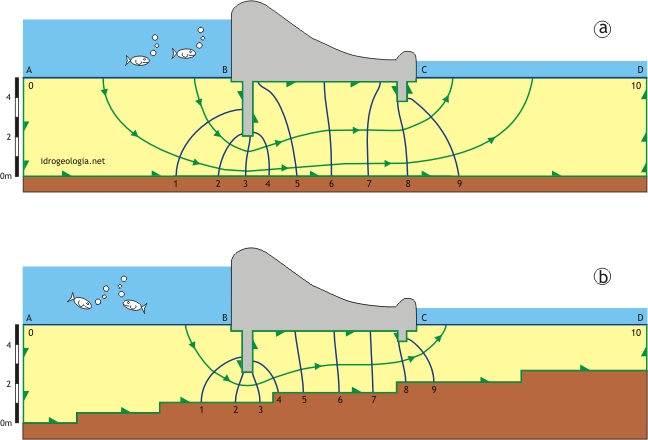
Fig. 2 – Esempi di reti di flusso in condizioni confinate con mazzo di filtrazione omogeneo ed isotropo. a) filtrazione al di sotto di una palancola, b) filtrazione al di sotto di una traversa fluviale con diaframmi, d) filtrazione al di sotto di una traversa fluviale con diaframmi e con base acquifero di profilo irregolare.
Anche se a monte e a valle della struttura di sbarramento l’acquifero è talmente esteso da poterlo considerare quasi illimitato, per il tracciamento della rete di flusso occorre definire graficamente una larghezza di disegno e di conseguenza occorre porre al modello dei limiti laterali. Visto che allontanandosi dalla struttura di sbarramento il contributo alla portata di filtrazione decresce, l’imposizione di un limite laterale impermeabile non influenza in modo significativo il risultato finale, a condizione ovviamente che questo limite sia posto ad una distanza sufficiente da non alterare l’andamento della rete di flusso. In linea di massima per una rete di flusso tracciata a mano, e quindi soggetta a tutti gli inevitabili errori grafici di disegno, una distanza fra limite laterale impermeabile e struttura di sbarramento di 2-4 volte lo spessore dell’acquifero può essere ritenuta sufficiente. Nei casi b, c e d di figura 1 il limite è stato posto ad una distanza dalla struttura impermeabile di circa 2 volte lo spessore dell’acquifero.
Definiti i limiti impermeabili e i limiti a carico idraulico costante si può procedere con il disegno della rete di flusso. Le indicazioni su come procedere [1]Custodio E. (2005): Teoria elementare di fluodinamica in mezzi porosi. In: Idrologia sotterranea, a cura di: Custodio E., Llamas M.R.. Dario Flaccovio Editore (Palermo), pp 429-586 – ISBN … Continue reading[2]Colleselli F., Colombo P. (1996): Elementi di Geotecnica. Zanichelli (Bologna), pp 1-500 – ISBN 88-08-09784-6[3]Harry R. Cedergren (1997): Seepage, Drainage, and Flow Nets. Wiley-IEEE, pp 1-496 – ISBN 047118053X[4]U.S.A.C.E. (1993): Seepage analysis and control for dams. U.S. Army Corps of Engineers (Washington) sono in generale abbastanza concordanti e in linea di massima si suggerisce di tracciare due o tre linee di flusso tenendo in considerazione che queste devono iniziare e terminare in corrispondenza dei due limiti a carico costante (AB e CD in figura 1 e 2) e che nel punto di intersezione con questi due limiti le linee di flusso devono formare angoli retti. Per realizzare il disegno è utile considerare che i limiti impermeabili del modello sono linee di flusso e pertanto le due linee di flusso superiore e inferiore risultano di fatto già tracciate.
Successivamente si procede tracciando qualche linea equipotenziale e tenendo in considerazione che queste devono iniziare e terminare in corrispondenza dei limiti impermeabili del modello, che in corrispondenza dei punti di intersezione con i limiti impermeabili devono formare angoli retti e che devono formare angoli retti in corrispondenza dell’intersezione con le linee di flusso tracciate in precedenza.
Dopo aver ottenuto per approssimazioni successive una perpendicolarità soddisfacente fra linee di flusso e linee equipotenziali si procede traslando le une e le altre in modo da realizzare una rete a maglie quadrate e ricavare una rete di flusso con caratteristiche idonee per il calcolo della portata di filtrazione.

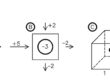
Fig. 3 – Zone della rete di flusso in cui è impossibile realizzare maglie quadrate. In figura queste zone sono indicate con colore giallo scuro ed evidenziate con un pallino rosso.
Si può anche iniziare tracciando le linee equipotenziali e poi le linee di flusso, ma questo procedimento può risultare meno intuitivo.
Esistono zone del modello nelle quali non è possibile realizzare una maglia quadrata. Ad esempio, nelle zone di figura 3 marcate con un pallino rosso, si ottengono maglie irregolari con 3, 5 e 6 lati. Questo problema è inevitabile e rientra nell’approssimazione del metodo.
La procedura manuale di disegno introduce inevitabili errori. Tuttavia nella pratica gli errori insiti nella determinazione del coefficiente di permeabilità sono sempre molto superiori rispetto agli errori grafici che si possono commettere nel disegno della rete di flusso e pertanto una rete anche realizzata con poche maglie e con una perpendicolarità non perfetta fra linee di flusso e linee equipotenziali può essere utilizzata per un calcolo preliminare della portata di filtrazione.
Attualmente il disegno della rete di flusso può essere facilitato dall’utilizzo di appositi software.
Ad esempio le reti riportate in queste schede sono state tracciate in modo manuale utilizzando come ausilio il software Modflow. La tabella seguente fornisce i valori di portata per metro di struttura per i 4 modelli riportati nelle figure 1 e 2. In tutti i modelli è stata sempre ipotizzata una differenza di carico fra AB e CD di 2 metri e per il mezzo di filtrazione è stato sempre assunto un coefficiente di permeabilità k = 1E-3 m/sec.
| Figura | Descrizione | Ne | Nf | q[m2/sec] |
| 1a | Palancola | 10 | 3,78 | 7,57E-4 |
| 1b | Traversa senza diaframmi | 10 | 3,23 | 6,46E-4 |
| 2a | Traversa con diaframmi | 10 | 2,28 | 4,57E-4 |
| 2b | Traversa con base acquifero irregolare | 10 | 1,75 | 3,51E-4 |
Per comodità nei disegni di delle figure 1 e 2 il tubo di flusso con maglia non quadrata è l’inferiore. Questo effetto è visibile in particolar modo nel caso 1b e nel caso 2a. Nei casi 1a e 2b il tubo inferiore ha ancora una maglia rettangolare ma, visto che i rapporti fra i lati dei rettangoli sono di 0,78 e 0,75, la maglia visivamente appare ancora quasi quadrata.
Bibliografia
| ↑1 | Custodio E. (2005): Teoria elementare di fluodinamica in mezzi porosi. In: Idrologia sotterranea, a cura di: Custodio E., Llamas M.R.. Dario Flaccovio Editore (Palermo), pp 429-586 – ISBN 88-7758-623-0 |
|---|---|
| ↑2 | Colleselli F., Colombo P. (1996): Elementi di Geotecnica. Zanichelli (Bologna), pp 1-500 – ISBN 88-08-09784-6 |
| ↑3 | Harry R. Cedergren (1997): Seepage, Drainage, and Flow Nets. Wiley-IEEE, pp 1-496 – ISBN 047118053X |
| ↑4 | U.S.A.C.E. (1993): Seepage analysis and control for dams. U.S. Army Corps of Engineers (Washington) |