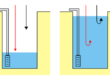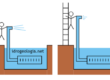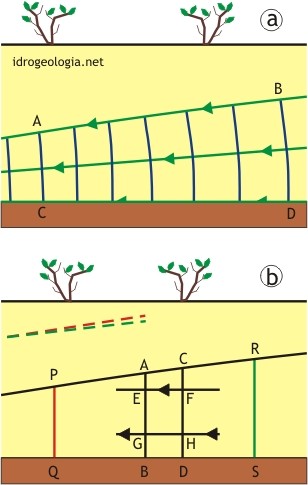
Fig. 1 – a: esempio di filtrazione in condizioni freatiche visualizzato mediante una rete di flusso (in verde: linee di flusso; in blu: linee equipotenziali); b: assunzioni semplificative di Dupuit-Forchheimer. In entrambe le figure la direzione di filtrazione, evidenziata dalle frecce, è da destra verso sinistra.
Il fenomeno della filtrazione prevede, come condizione necessaria, l’esistenza di una differenza di carico idraulico e in condizioni freatiche l’acqua, nella migrazione fra le aree di alimentazione e le aree di recapito, deve necessariamente abbassarsi di quota.
Uno schema molto semplice di filtrazione in condizioni freatiche è rappresentato in figura 1a tramite una rete di flusso. In questo modello l’acqua si sposta da destra verso sinistra e le linee di flusso, indicate in verde, sono inclinate verso la zona di recapito. Dall’esame della figura si può osservare che l’inclinazione è massima nella linea di flusso superiore, che corrisponde alla superficie freatica, si riduce nella linea di flusso intermedia e si azzera nella linea di flusso inferiore, che corrisponde alla base del modello. Per via di questa differenza di inclinazione, il tratto di linea di flusso AB risulta più lungo del tratto di linea di flusso CD. Posto che la perdita di carico fra A e B è uguale alla perdita di carico fra C e D, il gradiente idraulico medio lungo CD risulta maggiore rispetto al gradiente idraulico medio lungo AB. Come conseguenza, la velocità di filtrazione alla base del modello risulta maggiore rispetto alla velocità di filtrazione alla superficie.
Da questo semplice esempio emerge che lo studio della filtrazione in condizioni freatiche può risultare molto complicato in quanto esistono componenti di flusso sia in direzione orizzontale sia in direzione verticale ed esistono variazioni di velocità lungo la stessa verticale.
Utilizzando però una serie di assunzioni è possibile operare delle forti semplificazioni. Queste ipotesi vennero inizialmente elaborate da Dupuit[1]Dupuit, J (1863): Études Théoriques et Pratiques sur le Mouvement des Eaux dans les Canaux Découverts et à Travers les Terrains Perméables. Dunod, Paris e successivamente riprese da Forchheimer[2]Forchheimer, P. (1930): Hydraulik. Teubner Verlagsgesellschaft, Stuttgart e pertanto vengono generalmente indicate come assunzioni di Dupuit-Forchheimer.
Per poter applicare queste approssimazioni occorre che la superficie freatica sia poco inclinata e che la geometria del sistema sia tale da escludere una forte componente verticale nel moto di filtrazione.
In queste condizioni si assume che:
- Il moto di filtrazione avvenga unicamente in direzione orizzontale;
- il gradiente idraulico, che determina la velocità dell’acqua nei vari punti del modello, sia uguale all’inclinazione della superficie freatica.
La prima condizione determina a cascata altre due condizioni aggiuntive. Se infatti il moto di filtrazione è unicamente orizzontale le linee equipotenziali devono risultare verticali. Inoltre, se tutte le linee equipotenziali sono verticali, lungo una medesima verticale la velocità di filtrazione non cambia.
Facendo riferimento alla figura 1b, visto che le linee equipotenziali AB e CD sono verticali, il segmento EF è uguale al segmento GH. Posto che i due segmenti risultano di uguale lunghezza e che la perdita di carico alle estremità dei segmenti è la medesima, anche la velocità di filtrazione deve risultare la medesima.
La velocità di filtrazione però, varia spostandosi in senso orizzontale. In colore rosso e verde sono indicate due sezioni (PQ a valle e RS a monte) e con linee tratteggiate di uguale colore sono indicate le tangenti alla superficie freatica in P ed R. Dal disegno si osserva che in PQ la sezione di filtrazione è minore ma l’inclinazione della piezometrica è superiore mentre in RS la sezione di filtrazione è maggiore ma la superficie piezometrica risulta meno inclinata. Pertanto in corrispondenza della zona rossa si ha una trasmissività minore ma un gradiente maggiore e in corrispondenza della zona verde si ha una trasmissività maggiore ma un gradiente minore e questa combinazione consente di mantenere una continuità nel moto di filtrazione.
Le assunzioni di Dupuit-Forchheimer, sebbene rappresentino un potente strumento per la semplificazione dei calcoli, hanno una forte inconsistenza interna.
Perché possa esistere un moto di filtrazione è necessario un gradiente e per l’esistenza di un gradiente è necessaria una perdita di carico. In condizioni freatiche la perdita di carico impone uno spostamento delle particelle d’acqua da una quota più elevata verso una quota più bassa e questo contrasta con la prima assunzione, che prevede un moto di filtrazione unicamente orizzontale.
Malgrado questo però, le assunzioni di Dupuit-Forchheimer mantengono la loro validità [3]D. Kirkham (1967): Physical model for Dupuit-Forchheimer drainage theory. International Soil Water Symposium, June 5-11, Prague, Czechoslovakia. Czechoslovak National Committee of the International … Continue reading e l’errore nei calcoli è piccolo se i2<<1 [4]Lakshmi N. Reddi (2003): Seepage in soils: principles and applications. John Wiley and Sons, pp 1-402 – ISBN 0471356166[5]Daniel K. Sunada, David B. McWhorter (1977): Ground-water hydrology and hydraulics. Water Resources Publication, pp 1-290 – ISBN 0918334187.
Le assunzioni di Dupuit-Forchheimer vengono illustrate in tutti i principali testi che trattano della filtrazione delle acque sotterranee. A titolo puramente esemplificativo si possono indicare [6]J. Graham Herbertson, Peter Smart (1992): Drainage design. Taylor & Francis, pp 1-299 – ISBN 0216931568[7]Lakshmi N. Reddi (2003): Seepage in soils: principles and applications. John Wiley and Sons, pp 1-402 – ISBN 0471356166[8]Henk M. Haitjema (1995): Analytic element modeling of groundwater flow. Academic Press, pp 1-394 – ISBN 0123165504[9]Zekai Sen (1995): Applied hydrogeology for scientists and engineers. CRC Press, pp 1-444 – ISBN 1566700914[10]Bruce Misstear, David Banks, Lewis Clark (2006): Water wells and boreholes. John Wiley and Sons, pp 1-498 – ISBN 0470849894[11]Daniel K. Sunada, David B. McWhorter (1977): Ground-water hydrology and hydraulics. Water Resources Publication, pp 1-290 – ISBN 0918334187[12]Jacob Bear (1988): Dynamics of fluids in porous media. Courier Dover Publications, pp 1-764 – ISBN 0486656756[13]Jacques Willy Delleur (2007): The handbook of groundwater engineering. CRC Press, pp 1-1320 – ISBN 084934316X[14]D. J. Poehls, Gregory J. Smith (2009): Encyclopedic dictionary of hydrogeology. Academic Press, pp 1-517 – ISBN 0125586906 [474, 507] . In [15]Elias A. Rashmawi, Mark E. Grismer (1993): Dupuit-Forchheimer approximation may underestimate groundwater flow to San Joaquin River. California Agricolture, January-February, Vol 47 n. 1, pp 12-15 viene invece riportato un caso di non applicabilità delle assunzioni di Dupuit-Forchheimer per via dell’elevata componente verticale del flusso.
Bibliografia
| ↑1 | Dupuit, J (1863): Études Théoriques et Pratiques sur le Mouvement des Eaux dans les Canaux Découverts et à Travers les Terrains Perméables. Dunod, Paris |
|---|---|
| ↑2 | Forchheimer, P. (1930): Hydraulik. Teubner Verlagsgesellschaft, Stuttgart |
| ↑3 | D. Kirkham (1967): Physical model for Dupuit-Forchheimer drainage theory. International Soil Water Symposium, June 5-11, Prague, Czechoslovakia. Czechoslovak National Committee of the International Commission on Irrigation and Drainage, pp 385-395 |
| ↑4, ↑7 | Lakshmi N. Reddi (2003): Seepage in soils: principles and applications. John Wiley and Sons, pp 1-402 – ISBN 0471356166 |
| ↑5, ↑11 | Daniel K. Sunada, David B. McWhorter (1977): Ground-water hydrology and hydraulics. Water Resources Publication, pp 1-290 – ISBN 0918334187 |
| ↑6 | J. Graham Herbertson, Peter Smart (1992): Drainage design. Taylor & Francis, pp 1-299 – ISBN 0216931568 |
| ↑8 | Henk M. Haitjema (1995): Analytic element modeling of groundwater flow. Academic Press, pp 1-394 – ISBN 0123165504 |
| ↑9 | Zekai Sen (1995): Applied hydrogeology for scientists and engineers. CRC Press, pp 1-444 – ISBN 1566700914 |
| ↑10 | Bruce Misstear, David Banks, Lewis Clark (2006): Water wells and boreholes. John Wiley and Sons, pp 1-498 – ISBN 0470849894 |
| ↑12 | Jacob Bear (1988): Dynamics of fluids in porous media. Courier Dover Publications, pp 1-764 – ISBN 0486656756 |
| ↑13 | Jacques Willy Delleur (2007): The handbook of groundwater engineering. CRC Press, pp 1-1320 – ISBN 084934316X |
| ↑14 | D. J. Poehls, Gregory J. Smith (2009): Encyclopedic dictionary of hydrogeology. Academic Press, pp 1-517 – ISBN 0125586906 |
| ↑15 | Elias A. Rashmawi, Mark E. Grismer (1993): Dupuit-Forchheimer approximation may underestimate groundwater flow to San Joaquin River. California Agricolture, January-February, Vol 47 n. 1, pp 12-15 |