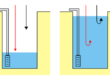
Il raggio di influenza è un concetto molto utilizzato in idrogeologia e può essere agevolmente compreso simulando di realizzare una prova di pompaggio protratta per lungo tempo.
Si immagina di disporre di un sistema costituito da un pozzo e da una serie di piezometri posti a distanza progressivamente crescente e, come in effetti capita nella realtà, di monitorare il comportamento dei piezometri nel procedere della prova.
Se l’acquifero è sufficientemente esteso, se non esistono altre fonti di perturbazione nelle vicinanze del pozzo di prova e se la prova è eseguita correttamente si osserva che:
- i piezometri più vicini si deprimono in misura maggiore rispetto ai più lontani;
- i massimi abbassamenti si registrano nelle fasi iniziali della prova;
- oltre un certo tempo, variabile da caso a caso, i piezometri tendono a stabilizzarsi ad una determinata quota e ad oscillare seguendo le naturali variazioni di livello dell’acquifero.
Questo insieme di osservazioni portano a concludere che:
- il pompaggio provoca una perturbazione nell’acquifero che è massima in prossimità dell’opera di drenaggio e si attenua con la distanza;
- oltre un certo limite di tempo il sistema trova un suo equilibrio e gli abbassamenti si stabilizzano.
Visto che la perturbazione si attenua con la distanza e che il sistema tende con il tempo a stabilizzarsi, si può ragionevolmente immaginare che esista un limite oltre il quale gli effetti del pompaggio non si risentono più, anche se il pozzo viene mantenuto in attività per molto tempo. Questa distanza viene definita raggio di influenza e varia da caso a caso in funzione del tipo di acquifero, del tipo di opera di captazione e della portata emunta. Se ad esempio a parità di altre condizioni si immagina di aumentare la portata del pozzo, si può ragionevolmente immaginare che questa distanza aumenti, mentre se si diminuisce la portata questa distanza diminuirà.
Il limite cioè si può allontanare o avvicinare dall’opera di drenaggio, ma deve sempre esistere. Questo concetto, intuitivo per il caso del pozzo, si può applicare ad una trincea drenante, ad una galleria, ad un sistema well-point e in generale a qualunque sistema destinato all’estrazione di acqua da una falda.
L’emungimento rappresenta sicuramente la causa più comune di perturbazione su un acquifero ma anche fenomeni di sbarramento artificiale, come ad esempio l’infissione di palancole, la realizzazione di opere interrate o la realizzazione di consolidamenti possono generare locali variazioni nella distribuzione dei carichi idraulici. Anche in questo caso però, allontanandosi dall’opera gli effetti sull’acquifero si risentono in modo sempre meno marcato e, oltrepassato un certo limite, questi effetti sono nulli o comunque non possono più essere rilevati.
Da un punto di vista idrogeologico il raggio di influenza di una determinata opera in determinate condizioni di funzionamento può quindi essere definito come la distanza oltre la quale gli effetti dell’opera sull’acquifero non sono più rilevabili.
Formule per il calcolo del raggio di influenza
Formula di Sichard
In letteratura esistono diverse formule empiriche e semiempiriche per il calcolo del raggio di influenza. La più comune, che si ritrova citata ad esempio in [1]Martin Preene, Pat M. Cashman (2001): Groundwater lowering in construction: a practical guide. Taylor & Francis, pp 1-476 – ISBN 0419211101[2]Lakshmi N. Reddi (2003): Seepage in soils: principles and applications. John Wiley and Sons, pp 1-402 – ISBN 0471356166[3]Zekai Sen (1995): Applied hydrogeology for scientists and engineers. CRC Press, pp 1-444 – ISBN 1566700914[4]CIRIA (1986): Control of groundwater for temporary works. Ciria Report n. 113, pp 1-87[5]Anand Prakash (2004): Water resources engineering: handbook of essential methods and design. ASCE Publications, pp 1-348 – ISBN 078440674X[6]Arthur B. Corwin, Christine J. Herridge, J. Patrick Powers, Paul C. Schmall (2007): Construction dewatering and groundwater control: new methods and applications. John Wiley and Sons, pp 1-638 … Continue reading[7]Zekai Sen (2008): Wadi hydrology. CRC Press, pp 1-347 – ISBN 1420061542[8]Ulrich Smoltczyk (2002): Geotechnical engineering handbook, Volume 2. Ernst & Sohn, pp 1-701 – ISBN 3433014507[9]J. D. Istok, Karen J. Dawson (1991): Aquifer testing: design and analysis of pumping and slug tests. CRC Press, pp 1-344 – ISBN 0873715012[10]Abdel-Mohsen Onsy Mohamed, Hogan E. Antia (1998): Geoenvironmental engineering. Elsevier, pp 1-707 – ISBN 0444898476[11]A. H.-D. Cheng (2000): Multilayered aquifer systems: fundamentals and applications. CRC Press, pp 1-384 – ISBN 0824798759[12]John Woodward (2005): An introduction to geotechnical processes. Taylor & Francis, pp 1-123 – ISBN 0415286468, è la formula di Sichard [13]Sichard, W (1927): Das Fassungsvermogen von Bohrbrunnen und seine Bedeutung fur die grundwassesabsenkung inbesondere fur grossere Absenktiefen. Diss. Technische Hochshule, Berlin in cui il raggio di influenza R (in metri), è calcolabile con l’equazione
dove Δh rappresenta l’abbassamento in metri registrato nel pozzo in seguito al pompaggio, k il {coefficiente di permeabilità} in m/sec e C una costante empirica che nel caso del pozzo singolo si assume uguale a 3000 e nel caso della fila singola di pozzi o della trincea drenante si assume variabile fra 1500 e 2000.
In presenza di un gruppo di pozzi realizzati a breve distanza l’uno dall’altro si può utilizzare la tecnica del pozzo equivalente. In questo caso, se il raggio del pozzo equivalente non è trascurabile, [14]Martin Preene, Pat M. Cashman (2001): Groundwater lowering in construction: a practical guide. Taylor & Francis, pp 1-476 – ISBN 0419211101 suggerisce di utilizzare la formula
dove re rappresenta il raggio del pozzo equivalente espresso in metri.
Considerando che esistono relazioni empiriche, come da esempio la {formula di Hazen}, che consentono di stimare il coefficiente di permeabilità k in funzione del D10, è possibile calcolare il raggio di influenza di un pozzo isolato conoscendo il D10 del mezzo di filtrazione e l’abbassamento registrato in seguito al pompaggio. Questo procedimento può essere eseguito manualmente calcolando prima k dal D10 e poi applicando la formula di Sichard, oppure utilizzando gli abachi riportati in [15]Lakshmi N. Reddi (2003): Seepage in soils: principles and applications. John Wiley and Sons, pp 1-402 – ISBN 0471356166[16]J. D. Istok, Karen J. Dawson (1991): Aquifer testing: design and analysis of pumping and slug tests. CRC Press, pp 1-344 – ISBN 0873715012.
Formula di Kussakin
Un secondo metodo per il calcolo empirico del raggio di influenza, riportato in [17]Anand Prakash (2004): Water resources engineering: handbook of essential methods and design. ASCE Publications, pp 1-348 – ISBN 078440674X[18]Ulrich Smoltczyk (2002): Geotechnical engineering handbook, Volume 2. Ernst & Sohn, pp 1-701 – ISBN 3433014507[19]Abdel-Mohsen Onsy Mohamed, Hogan E. Antia (1998): Geoenvironmental engineering. Elsevier, pp 1-707 – ISBN 0444898476, per le condizioni freatiche prevede l’utilizzo della formula
dove R rappresenta il raggio di influenza, Δh l’abbassamento registrato nel pozzo in seguito al pompaggio, k il coefficiente di permeabilità e H il {carico idraulico} indisturbato.
In condizioni artesiane si applica
dove D rappresenta lo spessore dell’acquifero.
Nelle due formule le lunghezze (Δh, H e D) sono espresse in metri e la permeabilità in metri/sec.
Calcolo del raggio di influenza in funzione della ricarica
Se in un acquifero è nota l’intensità di ricarica, si può utilizzare la formula
riportata in [20]Abdel-Mohsen Onsy Mohamed, Hogan E. Antia (1998): Geoenvironmental engineering. Elsevier, pp 1-707 – ISBN 0444898476[21]A. H.-D. Cheng (2000): Multilayered aquifer systems: fundamentals and applications. CRC Press, pp 1-384 – ISBN 0824798759, dove R rappresenta il raggio di influenza, H lo spessore dell’acquifero saturo e w l’intensità di ricarica.
Introduzione del raggio di influenza nelle formule analitiche
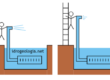
Una delle applicazioni più comuni del raggio di influenza riguarda lo studio del comportamento del pozzo isolato, cioè perforato in un’area distante da qualunque fonte di perturbazione. Il caso tipico prevede che un pozzo sia realizzato in un acquifero indefinitamente esteso con falda perfettamente orizzontale, che il pompaggio sia mantenuto perfettamente costante per un tempo indefinitamente lungo e che nell’acquifero non esista altra fonte di alimentazione o drenaggio ad eccezione del pozzo oggetto dello studio. Un problema posto in questi termini sarebbe irrisolvibile in condizioni stazionarie in quanto in assenza di una ricarica il pozzo drenerebbe progressivamente tutto l’acquifero. In questo caso per risolvere il problema si suppone che attorno al pozzo sia realizzato un canale circolare concentrico al pozzo, si suppone che il livello dell’acqua nel canale sia mantenuto sempre alla medesima quota e si suppone inoltre che le pareti del canale siano prive di rivestimento, in modo cioè che sia possibile uno scambio di acqua fra il canale e l’acquifero.
Con questa assunzione il modello diventa risolvibile in quanto il canale può cedere un quantitativo d’acqua pari a quello estratto dal pozzo e in questo modo il sistema diventa bilanciato.
Il canale immaginario, che nel modello rappresenta la condizione al contorno a carico idraulico costante, costituisce anche una barriera alla propagazione degli effetti del drenaggio. Nei modelli realizzati in questo modo infatti, all’esterno del canale gli effetti del pompaggio non si risentono più e pertanto il raggio di questo canale circolare rappresenta sostanzialmente il raggio di influenza del pozzo. La differenza fra il modello e la realtà è che nel modello la distanza pozzo-canale viene scelta arbitrariamente mentre nella realtà il raggio di influenza dipende da una serie di fattori ed è approssimativamente calcolabile con le formule empiriche descritte in precedenza.
Per trasportare le formule analitiche nella realtà occorre quindi sostituire la distanza fra l’opera di drenaggio e la condizione al contorno con il raggio di influenza e imporre alla condizione al contorno un carico idraulico uguale al carico idraulico registrato nell’opera di drenaggio prima dell’inizio del pompaggio, cioè il carico idraulico in condizioni indisturbate.
Perché esiste il raggio di influenza
Confrontando i modelli teorici di emungimento di un pozzo o di una trincea isolati con le osservazioni sperimentali si osserva una discrepanza. In teoria l’emungimento in una falda priva di alimentazione porta al progressivo prosciugamento dell’acquifero, ma in pratica se un pozzo è perforato in un acquifero sufficientemente esteso, propaga i suoi effetti solo in un raggio limitato, anche se viene mantenuto in attività per molto tempo. La ragione deriva dal fatto che gli acquiferi naturali hanno sempre un loro dinamica e le complesse interazioni fra ricariche e perdite determinano delle continue oscillazioni dei livelli di falda. L’interazione di questi fattori fa si che il livello indisturbato dell’acquifero non sia statico ma oscilli attorno ad un valore medio e questa situazione è ben visibile se, prima dell’inizio del pompaggio, si mantiene monitorato il livello del pozzo per un certo tempo. Queste oscillazioni determinano una sorta di rumore di fondo che, nel momento in cui il pozzo entra in funzione, vanno a sovrapporsi agli effetti dovuti al pompaggio. Visto che la perturbazione prodotta dal pompaggio diminuisce di intensità allontanandosi dall’asse del pozzo, oltrepassata una certa distanza non è più possibile distinguere gli abbassamenti dovuti al pompaggio dalle normali oscillazioni dell’acquifero. In pratica cioè ad una certa distanza dall’opera il rumore di fondo diventa talmente rilevante in confronto agli abbassamenti provocati dal pompaggio da mascherarli completamente. Questa distanza, che risulta influenzata dalle caratteristiche dell’acquifero, dalla portata di emungimento e dalla dinamica dell’acquifero nel suo complesso, rappresenta appunto il raggio di influenza, osservabile sperimentalmente nella realtà posizionando attorno all’opera di drenaggio una serie di punti di monitoraggio posti ad una distanza progressivamente crescente.
Bibliografia
| ↑1, ↑14 | Martin Preene, Pat M. Cashman (2001): Groundwater lowering in construction: a practical guide. Taylor & Francis, pp 1-476 – ISBN 0419211101 |
|---|---|
| ↑2, ↑15 | Lakshmi N. Reddi (2003): Seepage in soils: principles and applications. John Wiley and Sons, pp 1-402 – ISBN 0471356166 |
| ↑3 | Zekai Sen (1995): Applied hydrogeology for scientists and engineers. CRC Press, pp 1-444 – ISBN 1566700914 |
| ↑4 | CIRIA (1986): Control of groundwater for temporary works. Ciria Report n. 113, pp 1-87 |
| ↑5, ↑17 | Anand Prakash (2004): Water resources engineering: handbook of essential methods and design. ASCE Publications, pp 1-348 – ISBN 078440674X |
| ↑6 | Arthur B. Corwin, Christine J. Herridge, J. Patrick Powers, Paul C. Schmall (2007): Construction dewatering and groundwater control: new methods and applications. John Wiley and Sons, pp 1-638 – ISBN 0471479438 |
| ↑7 | Zekai Sen (2008): Wadi hydrology. CRC Press, pp 1-347 – ISBN 1420061542 |
| ↑8, ↑18 | Ulrich Smoltczyk (2002): Geotechnical engineering handbook, Volume 2. Ernst & Sohn, pp 1-701 – ISBN 3433014507 |
| ↑9, ↑16 | J. D. Istok, Karen J. Dawson (1991): Aquifer testing: design and analysis of pumping and slug tests. CRC Press, pp 1-344 – ISBN 0873715012 |
| ↑10, ↑19, ↑20 | Abdel-Mohsen Onsy Mohamed, Hogan E. Antia (1998): Geoenvironmental engineering. Elsevier, pp 1-707 – ISBN 0444898476 |
| ↑11, ↑21 | A. H.-D. Cheng (2000): Multilayered aquifer systems: fundamentals and applications. CRC Press, pp 1-384 – ISBN 0824798759 |
| ↑12 | John Woodward (2005): An introduction to geotechnical processes. Taylor & Francis, pp 1-123 – ISBN 0415286468 |
| ↑13 | Sichard, W (1927): Das Fassungsvermogen von Bohrbrunnen und seine Bedeutung fur die grundwassesabsenkung inbesondere fur grossere Absenktiefen. Diss. Technische Hochshule, Berlin |