Il modello di riferimento per lo studio della filtrazione verso un pozzo artesiano è indicato nello schema tridimensionale di fig. 1.
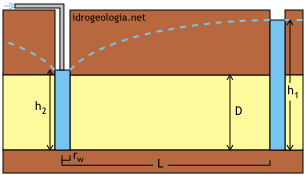
Si suppone che in un acquifero artesiano di spessore D, rappresentato in figura in colore giallo, sia realizzato un pozzo completo, perforato cioè fino alla base dell’acquifero. Si suppone inoltre che ad una distanza L dall’asse del pozzo artesiano sia presente un canale di forma circolare e si suppone che il livello dell’acqua nel canale venga mantenuto sempre costante.
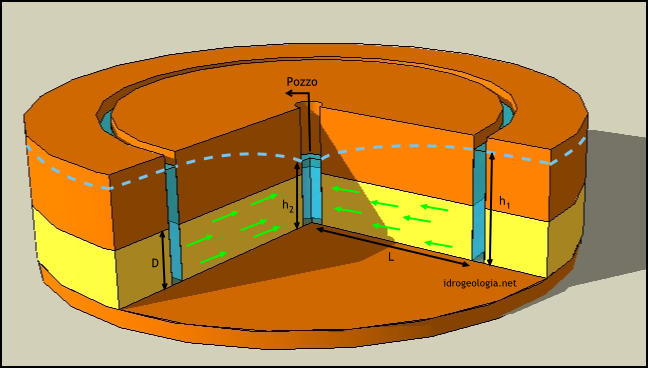
Fig. 1 – Schema di riferimento per lo studio della filtrazione in regime stazionario verso un pozzo artesiano.
Prendendo come zero di riferimento la base dell’acquifero, ed assumendo che il livello dell’acqua nel canale sia h1, in assenza di pompaggio anche l’acqua nel pozzo artesiano si stabilizza alla quota h1. Se si attiva la pompa il livello nel pozzo artesiano si deprime fino alla quota h2 e come conseguenza di instaura un moto di filtrazione radiale diretto dal canale verso il pozzo.
Facendo riferimento alla figura 2, ad una distanza r dall’asse del pozzo la sezione di filtrazione risulta
Visto che ad una distanza generica r dall’asse del pozzo il {gradiente idraulico} i si può esprimere con la relazione
considerando la legge fondamentale dell’idrogeologia
si ricava
che conduce a
Integrando si ottiene
con C costante di integrazione.
Considerando che per r = rw si ha h = h2 e che per r = L si ha h = h1 si ricava
Ponendo
si perviene alla formula
che consente di calcolare la portata di filtrazione verso un pozzo in condizioni artesiane note le condizioni al contorno, la geometria del problema e l’abbassamento registrato nel pozzo in seguito al pompaggio. In letteratura questa formula viene definita anche equazione di Thiem o formula di Thiem.
Analogamente al caso illustrato per la {trincea in condizioni artesiane}, utilizzando il concetto di {raggio di influenza} si può estendere il procedimento appena illustrato al caso del pozzo isolato. In queste condizioni la portata è calcolabile con la formula
dove Δh rappresenta sempre l’abbassamento registrato nel pozzo artesiano in seguito al pompaggio e R il raggio di influenza del pozzo.
Utilizzando l’Eq* è possibile calcolare il {carico idraulico} ad una qualunque distanza r dall’asse del pozzo con la condizione
Sostituendo al posto di h2 il carico idraulico generico h e al posto di rw la distanza generica r si ottiene
e quindi si ricava
L’equazione è del tipo
e pertanto si conclude che il carico idraulico varia in funzione del logaritmo della distanza dall’asse del pozzo artesiano.
Il confronto con il caso della {trincea drenante in condizioni artesiane} mostra una differenza nel profilo della linea equipotenziale congiungente l’area sorgente con l’area di recapito. Nel caso della trincea drenante infatti questa linea è un segmento di retta mentre nel caso del pozzo è una curva logaritmica. La spiegazione deriva dal fatto che nel caso della trincea drenante la sezione di filtrazione resta costante spostandosi dalla zona di alimentazione alla zona di recapito e quindi anche la velocità di filtrazione deve mantenersi costante.
Nel caso del pozzo artesiano la sezione di filtrazione diminuisce progressivamente spostandosi dal canale circolare, che rappresenta la zona di alimentazione, alle pareti esterne del pozzo che rappresentano la zona di recapito. Di conseguenza, per mantenere costante la portata, la velocità di filtrazione deve aumentare progressivamente avvicinandosi al pozzo e pertanto l’inclinazione della piezometrica deve aumentare spostandosi dalla zona di alimentazione verso la zona di recapito.
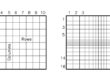
Per visualizzare graficamente questo fenomeno può essere utile esaminare la rete di flusso, rappresentata in figura 3.
Le linee equipotenziali sono anelli concentrici che tendono ad infittirsi avvicinandosi al pozzo e le linee di flusso sono segmenti radiali rispetto all’asse del pozzo.
Contrariamente ai casi illustrati nella scheda relativa alla {costruzione delle reti di flusso}, per il pozzo artesiano il disegno deve essere realizzato nel piano orizzontale. Per realizzare una rete di flusso occorre infatti che non esista una componente di filtrazione perpendicolare al piano di disegno e, per via della condizione di moto radiale che caratterizza il caso del pozzo artesiano, questa condizione si verifica solamente nel piano orizzontale.
Anche in questo caso con la rete di flusso si ottiene la portata per unità di lunghezza di struttura drenante. Per ottenere la portata complessiva, nel caso del pozzo artesiano completamente penetrante occorre moltiplicare il risultato ricavato con la rete di flusso per lo spessore dell’acquifero.
Video relativi alla scheda