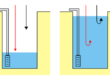
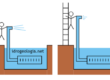
Lo schema tipo per lo studio di questo modello di filtrazione è rappresentato in figura 1. Analogamente al caso della {trincea artesiana} l’acqua filtra dal canale posto a destra verso la trincea drenante posta a sinistra ma in questo caso, per via della mancanza del livello impermeabile al tetto dell’acquifero, la filtrazione avviene in condizioni freatiche. Lo spessore saturo è massimo a destra, in corrispondenza del segmento AB, ed è minimo a sinistra, in corrispondenza del segmento CD. Visto che la filtrazione avviene in condizioni freatiche le linee di flusso sono inclinate da destra verso sinistra. Nel moto di filtrazione esiste una componente verticale che era assente in {condizioni artesiane} e pertanto per studiare il problema è conveniente utilizzare le {assunzioni semplificative di Dupuit-Forchheimer}.
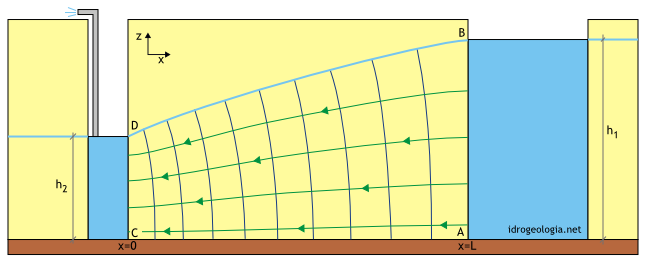
Fig 1 – Filtrazione in condizioni stazionarie verso una trincea drenante completa alimentata lateralmente in condizioni freatiche. In giallo: mezzo permeabile; in marrone: mezzo impermeabile.
In queste condizioni semplificate la componente verticale del moto di filtrazione viene ignorata e la velocità di filtrazione, costante in senso verticale, viene considerata proporzionale all’inclinazione della superficie freatica. La portata in corrispondenza di una qualunque verticale compresa fra x=0 e x=L risulta quindi
![]()
dove la derivata
![]()
rappresenta l’inclinazione della superficie freatica.
Risolvendo l’equazione si ottiene
![]()
con C che rappresenta la costante di integrazione.
Ricordando che per x=0 si ha h=h2 e che per x=L si ha h=h1, con la prima sostituzione ricava:
![]()
da cui
![]() Eq*
Eq*
e con la seconda sostituzione si ricava
![]()
e da qui si perviene infine alla formula
che consente di calcolare la portata di filtrazione verso la trincea drenante. La formula consente di calcolare la portata per unità di lunghezza di struttura e quindi, analogamente al caso precedente, il risultato ha le dimensioni [L2T-1].
Inserendo l’ultima equazione in quella precedentemente indicata con Eq * si ricava
![]()
e si perviene a
![]()
Mediante quest’ultima equazione, se si attribuiscono ad x valori compresi fra 0 e L, si può ricostruire per punti l’andamento della curva DB.
Occorre ricordare però, che la curva DB non rappresenta il reale andamento della superficie freatica, ma rappresenta l’andamento della superficie freatica nelle assunzioni semplificative di Dupuit-Forchheimer utilizzate per lo sviluppo dei calcoli.
In realtà non sempre la quota del punto D coincide con la quota del pelo libero dell’acqua nella trincea e pertanto la reale superficie freatica può essere differente da quella calcolata con questo procedimento.
Il fenomeno si verifica in misura tanto più rilevante quanto più il punto D si avvicina al punto C. Se infatti il segmento CD si riduce di lunghezza, la velocità di filtrazione in prossimità della trincea deve aumentare. Se per assurdo il punto D arrivasse quasi a coincidere con il punto C la velocità di filtrazione dovrebbe aumentare quasi all’infinito e questo ovviamente non è possibile. Nella realtà se il rapporto fra h2 e h1 è elevato e se il rapporto fra L e h1 è basso, in pratica cioè se esiste un elevato gradiente, in prossimità della trincea si sviluppa una superficie di trasudamento e il punto D si eleva ad una quota superiore alla quota del pelo libero dell’acqua nella trincea. In queste condizioni il calcolo della superficie freatica basato sulle assunzioni di Dupuit-Forckkeimer non è corretto in quanto, sopratutto in prossimità della trincea, fornisce valori di quota piezometrica inferiore a quelli reali.
Analogamente al caso precedente, utilizzando il concetto di {raggio di influenza} si può estendere l’Eq ** al problema della trincea isolata. La portata drenata per metro di struttura si può calcolare con la formula
dove H0 e R rappresentano rispettivamente il {carico idraulico} indisturbato, cioè in condizioni di assenza di pompaggio, e il raggio di influenza della trincea drenante.
Per le ragioni {precedentemente esposte}, rispetto al caso della trincea alimentata lateralmente da un canale, la portata viene raddoppiata.
Video relativi alla scheda