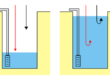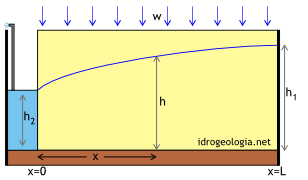
Fig 1 – Filtrazione verso una trincea drenante in condizioni freatiche. L’acquifero è alimentato verticalmente, con una intensità di alimentazione w. In giallo: mezzo permeabile; in marrone: mezzo impermeabile.
La figura 1 illustra uno schema tipo di filtrazione verso una trincea drenante alimentata verticalmente. Nello schema l’acqua, che ad esempio potrebbe provenire da precipitazioni meteoriche, filtra verticalmente attraverso la zona insatura fino a raggiungere la falda. In condizioni di assenza di drenaggio il livello della falda aumenterebbe progressivamente fino a raggiungere la superficie determinando di conseguenza la formazione di uno stagno ma la trincea drenante, che nello schema si trova a sinistra, drena progressivamente l’acqua di pioggia e il sistema raggiunge un equilibrio fra infiltrazione verticale e deflusso orizzontale. Nel modello si suppone che in corrispondenza del lato destro esista una barriera impermeabile che limita lateralmente il problema.
In queste condizioni [1]Jacques Delleur (1999): The Handbook of Groundwater Engineering. CRC Press, pp 1-940 – ISBN 3-540-64745-7[2]Jacques Willy Delleur (2007): The handbook of groundwater engineering. CRC Press, pp 1-1320 – ISBN 084934316X[3]Daniel K. Sunada, David B. McWhorter (1977): Ground-water hydrology and hydraulics. Water Resources Publication, pp 1-290 – ISBN 0918334187[4]Béla G. Lipták, David H. F. Liu (2000): Groundwater and surface water pollution. CRC Press, pp 1-150 – ISBN 1566705118[5]Custodio E., Galofrè A. (2005): Idraulica della captazioni di acque sotterranee. In: Idrologia sotterranea, a cura di: Custodio E., Llamas M.R.. Dario Flaccovio Editore (Palermo), pp 593-952 … Continue reading, posto che l’alimentazione verticale espressa in [LT-1] sia uniforme su tutta l’area e che la distanza fra la trincea e il limite laterale impermeabile sia L, è possibile calcolare la portata di deflusso alla distanza x dalla trincea con la formula:
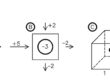
In corrispondenza della sezione posta ad una distanza x dalla trincea deve infatti defluire una portata uguale alla portata che si infiltra nel tratto a monte del punto x.
Utilizzando le approssimazioni di {Dupuit-Forchheimer} la portata in x si può anche esprimere come
Combinando le due equazioni si ottiene
che risolta conduce a
con C che rappresenta la costante di integrazione.
Considerando che per x=0 si ha h=h2 e che per x=L si ha h=h1, sostituendo i valori si ricava l’equazione
che consente di determinare la quota della piezometrica alla distanza L dalla trincea drenante.
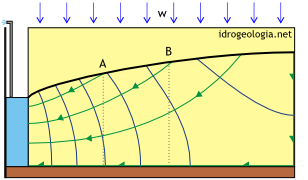
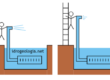
Fig. 2 – Rappresentazione mediante rete di flusso del processo di filtrazione verso una trincea drenante in acquifero freatico con alimentazione verticale. In verde: linee di flusso; in blu: linee equipotenziali; in nero: superficie freatica.
Contrariamente al caso della {trincea alimentata lateralmente}, la superficie freatica di fig. 2 non è una linea di flusso. L’acqua infatti raggiunge la superficie freatica per percolazione attraverso la zona insatura e, raggiunta la falda, costituisce alimentazione al drenaggio orizzontale imposto dalla presenza della trincea drenante.
La figura evidenzia l’intersezione fra le linee di flusso e la superficie freatica. Questo aspetto un po’ atipico della rete di flusso deriva dal fatto che la portata del sistema diminuisce dalla zona in prossimità della trincea, dove è massima, alla zona in prossimità del limite impermeabile, dove è nulla e come conseguenza anche il numero di tubi di flusso deve diminuire spostandosi da valle verso monte. Ad esempio, facendo riferimento ai punti A e B si osserva che la verticale passante per A intercetta tre tubi di flusso mentre la verticale passante per B ne intercetta solamente due. La progressiva estinzione dei tubi di flusso spostandosi da sinistra verso destra visualizza graficamente il processo descritto precedentemente e cioè il progressivo aumento delle portate drenate spostandosi da monte verso valle.
Bibliografia
| ↑1 | Jacques Delleur (1999): The Handbook of Groundwater Engineering. CRC Press, pp 1-940 – ISBN 3-540-64745-7 |
|---|---|
| ↑2 | Jacques Willy Delleur (2007): The handbook of groundwater engineering. CRC Press, pp 1-1320 – ISBN 084934316X |
| ↑3 | Daniel K. Sunada, David B. McWhorter (1977): Ground-water hydrology and hydraulics. Water Resources Publication, pp 1-290 – ISBN 0918334187 |
| ↑4 | Béla G. Lipták, David H. F. Liu (2000): Groundwater and surface water pollution. CRC Press, pp 1-150 – ISBN 1566705118 |
| ↑5 | Custodio E., Galofrè A. (2005): Idraulica della captazioni di acque sotterranee. In: Idrologia sotterranea, a cura di: Custodio E., Llamas M.R.. Dario Flaccovio Editore (Palermo), pp 593-952 – ISBN 88-7758-623-0 |