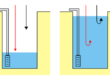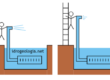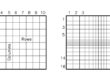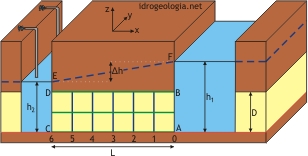
Fig. 1 – Schema tridimensionale di filtrazione verso una trincea drenante in condizioni artesiane. In giallo: mezzo permeabile; in marrone: mezzo impermeabile
Il problema della filtrazione verso una trincea drenante alimentata lateralmente in condizioni artesiane è schematizzato in figura 1. Si suppone che in un acquifero confinato, indefinitamente esteso isotropo e omogeneo sia realizzata una trincea completa e si suppone che parallelamente alla trincea, ad una distanza L, si trovi un canale a sviluppo rettilineo e ad andamento parallelo rispetto alla trincea che penetra fino alla base dell’acquifero. Il livello dell’acqua nel canale si suppone costante e superiore al tetto dell’acquifero. Il drenaggio della falda viene effettuato dalla trincea e si suppone che anche il livello dell’acqua nella trincea non scenda al di sotto del tetto dell’acquifero.
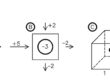
Il sistema si suppone indefinitamente esteso nel senso della lunghezza. Per questa ragione la componente della filtrazione lungo l’asse y è nulla e il problema può essere studiato esaminando unicamente il piano xz (fig. 2).
In questo semplice modello le linee AC e BD rappresentano i limiti impermeabili e le linee AB e CD rappresentano le condizioni al contorno a carico idraulico costante. Immaginando di indicare come quota zero di riferimento del modello la base dell’acquifero, il {carico idraulico} in AB è uguale ad h1 e il carico idraulico in CD è uguale da h2. Visto la geometria del problema la realizzazione della rete di flusso risulta immediata e porta al disegno di una maglia quadrata secondo lo schema di fig. 2.
Dallo schema, analogo a quello riportato in {esempio elementare di rete di flusso} emerge che le linee di flusso sono tutte orizzontali e le linee equipotenziali sono tutte verticali ed equispaziate. Posto che le linee equipotenziali risultano equispaziate si deduce che il gradiente idraulico fra AB e CD sia ovunque costante e pertanto si può concludere che la superficie piezometrica sia rappresentata dal segmento EF. Il calcolo della portata può a questo punto essere eseguito applicando semplicemente la legge di Darcy.
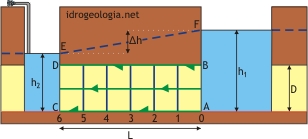
Fig. 2 – Schema bidimensionale di filtrazione verso una trincea drenante in condizioni artesiane. In verde: linee di flusso; in blu: linee equipotenziali; in blu a tratteggio: andamento della piezometrica.
Ricordando che
considerando una lunghezza unitaria di trincea si ricava la formula
dove
L’equazione ha le dimensioni L2T-1 e pertanto consente di calcolare la portata per unità di lunghezza di struttura drenante.
Applicando la formula per il calcolo della portata in una rete di flusso si perviene al medesimo risultato.
Indicando con Ne ed Nf rispettivamente il numero delle linee equipotenziali ed il numero dei tubi di flusso, facendo riferimento allo schema di figura 2 per ottenere una maglia quadrata occorre che
Ricordando che in un modello risolto con la rete di flusso {la portata è calcolabile con la formula}
facendo riferimento allo schema di figura 2 si ottiene nuovamente la formula
uguale a quella ricavata in precedenza.
Utilizzando il concetto di {raggio di influenza} si può estendere il procedimento al caso della trincea isolata. Se cioè in un acquifero artesiano è realizzata una trincea e se il livello dell’acqua nella trincea è superiore al limite impermeabile superiore dell’acquifero si può calcolare la portata drenata per metro di struttura con la formula
dove Δh e R rappresentano rispettivamente l’abbassamento registrato nella trincea in seguito al pompaggio e il raggio di influenza della trincea drenante.
Le formule che implicano la presenza del canale di alimentazione prevedono l’alimentazione della trincea solamente dal lato rivolto verso il canale. Nel caso della trincea isolata si suppone che l’alimentazione provenga in modo uguale da entrambi i lati e quindi nell’ultima formula compare il valore moltiplicativo 2.
Video relativi alla scheda